### 树的定义 - 由 $ n(n \geq 0) $ 个结点组成的有限集合 $ T $ - 当 $ n = 0 $ 时称为空树 - 在非空树中有且仅有一个根 (Root) 结点 - 其余结点可以分为 $ m(m \geq 0) $ 个互不相交的有限集 $ T\_1, T\_2, \cdots, T\_m $ - 其中每个集合称为根的子树 (SubTree)

### 树的特点 - 每个结点有零个或多个后继结点 - 每个结点有且只有一个前驱结点 (根节点例外) - 数据结点按分支关系组织 - 反映数据元素的层次关系 - 反映数据元素的一对多关系

### 树的抽象数据类型 ADT Tree { 数据对象 $ D = \lbrace a\_i | 0 \leq i \leq n - 1, n \geq 0, a\_i 为 E 类型 \rbrace $ 数据关系 $ r = \lbrace < a\_i, a\_j > | a\_i, a\_j \in D, 0 \leq i, j \leq n - 1 \rbrace $ 基本运算 boolean CreateTree() String toString() E GetParent(int i) }

### 树的逻辑结构表示方法 - 树形表示法 - 文氏图表示法 - 凹入表示法 - 括号表示法

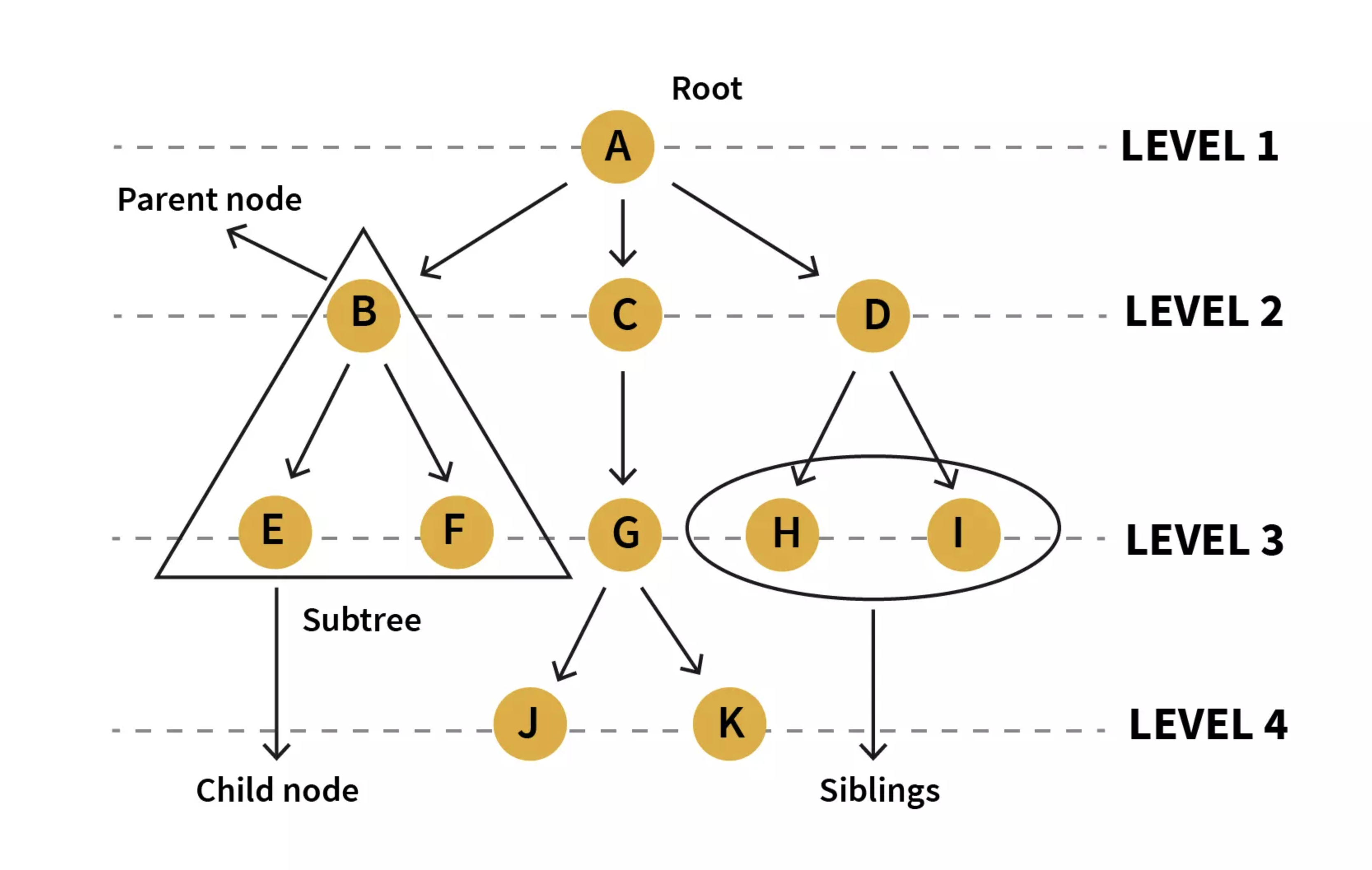
 #### Tree

### 树的基本术语 - 结点的度 Degree: 某个结点的子树的个数 - 树的度: 树中结点度的最大值 - 分支结点 Internal Nodes: 度不为零的结点 - 终端结点 Leaf Nodes: 度为零的结点

- 路径 Path: 从任意两个结点 $ a\_i $ 到 $ a\_j $ 的路径是一个结点序列 $ a\_i, a\_{i+1}, a\_{i+2}, \cdots, a\_j $ - 路径的长度 Length: 路径上的结点数目 $ -1 $

- 孩子结点 Child: 结点 $ a\_i $ 的后继结点称为 $ a\_i $ 的孩子结点 - 双亲结点 Parent: 结点 $ a\_i $ 是结点 $ a\_j $ 的孩子结点, 则称 $ a\_j $ 是 $ a\_i $ 的双亲结点 - 兄弟结点 Siblings: 具有同一双亲结点的结点互称为兄弟结点

- 结点的层次 Level: 根结点的层次为 $ 1 $, 其余结点的层次等于该结点的双亲结点的层次加 $ 1 $ - 树的高度 Height: 结点的最大层次

- 有序树 Ordered Tree: 树中结点的各子树从左到右是有次序的 - 无序树 Unordered Tree: 树中结点的各子树从左到右是无次序的 - 森林 Forest: $ m(m \geq 0) $ 棵互不相交的树的集合

### 树的性质 1 - 树中结点的个数等于所有结点的度数加 $ 1 $

### 树的性质 2 - 度为 $ m $ 的树中第 $ i $ 层上最多有 $ m^{i-1} $ 个结点 $ (i \geq 1) $

### 树的性质 3 - 高度为 $ h $ 的 $ m $ 次树最多有 $ \frac{m^h - 1}{m - 1} $ 个结点 $ (h \geq 1, m \geq 2) $

### 树的性质 4 - 具有 $ n $ 个结点的 $ m $ 次树的最小高度为 $ \lceil log_m(n(m - 1) + 1) \rceil $, 其中 $ \lceil x \rceil $ 表示不小于 $ x $ 的最小整数 (Ceiling)

### 树的基本运算 - 查找 - 插入或删除 - 遍历

### 遍历 - 深度优先, DFS, Depth First Search - 广度优先, BFS, Breath First Search

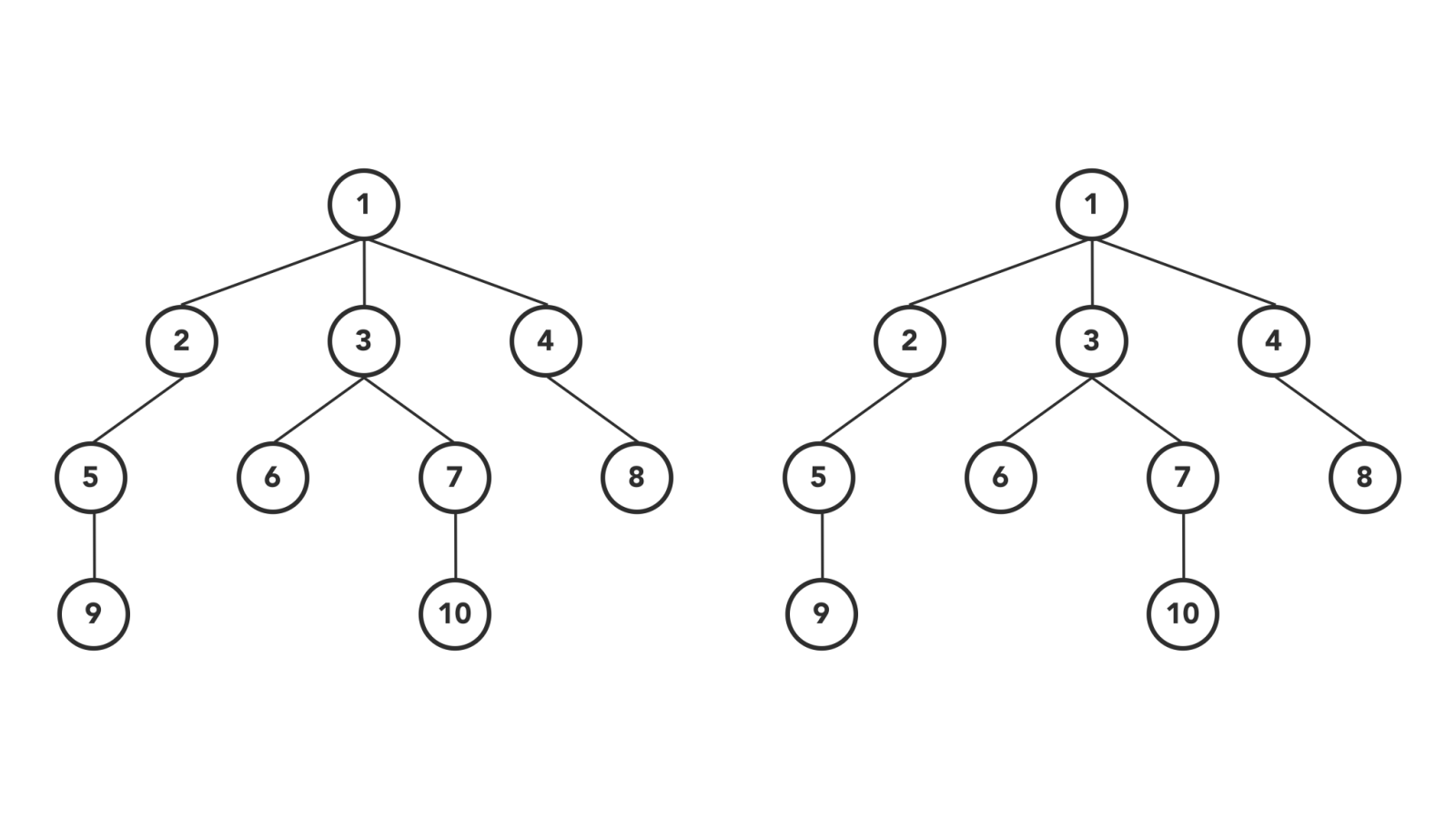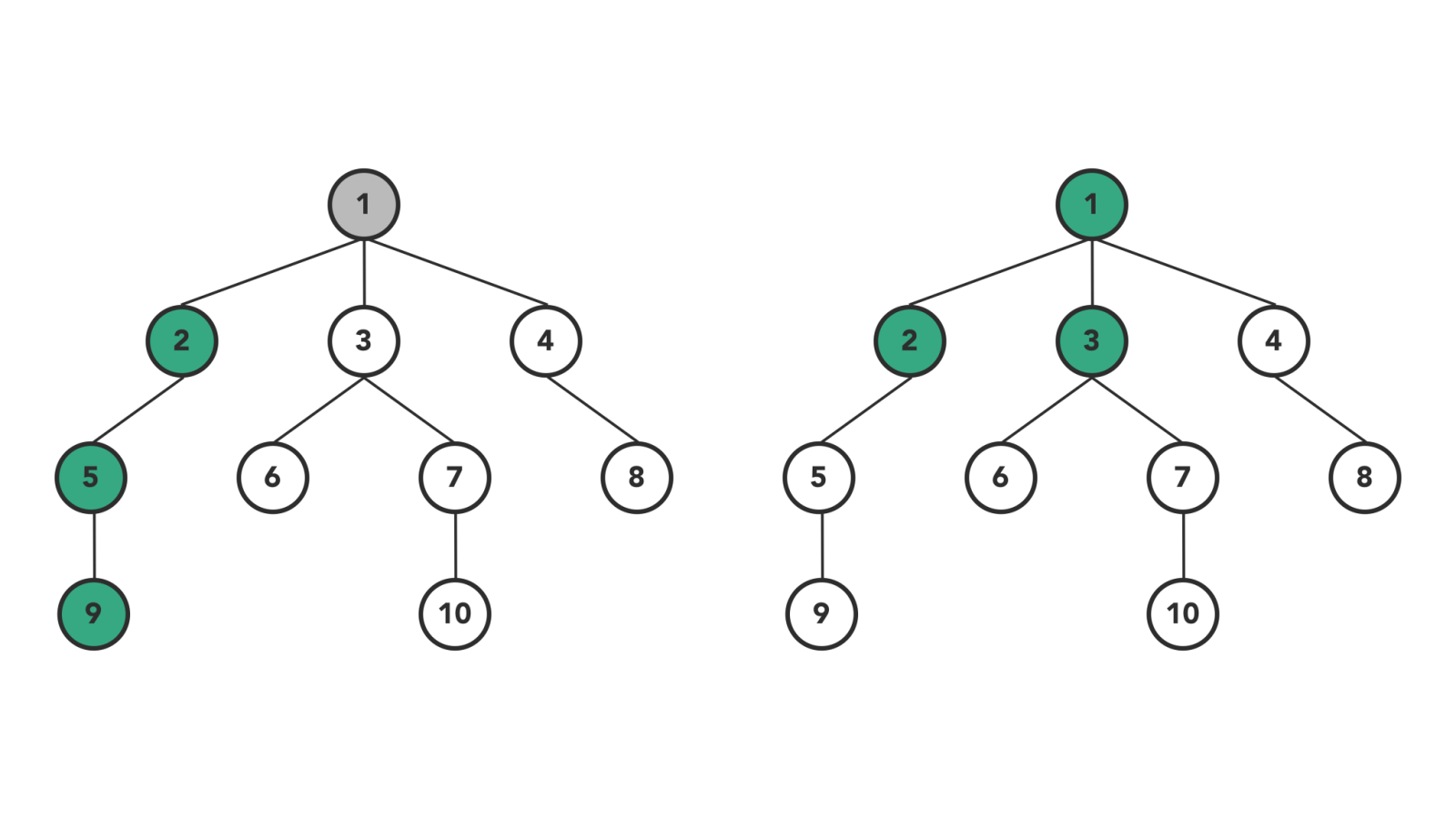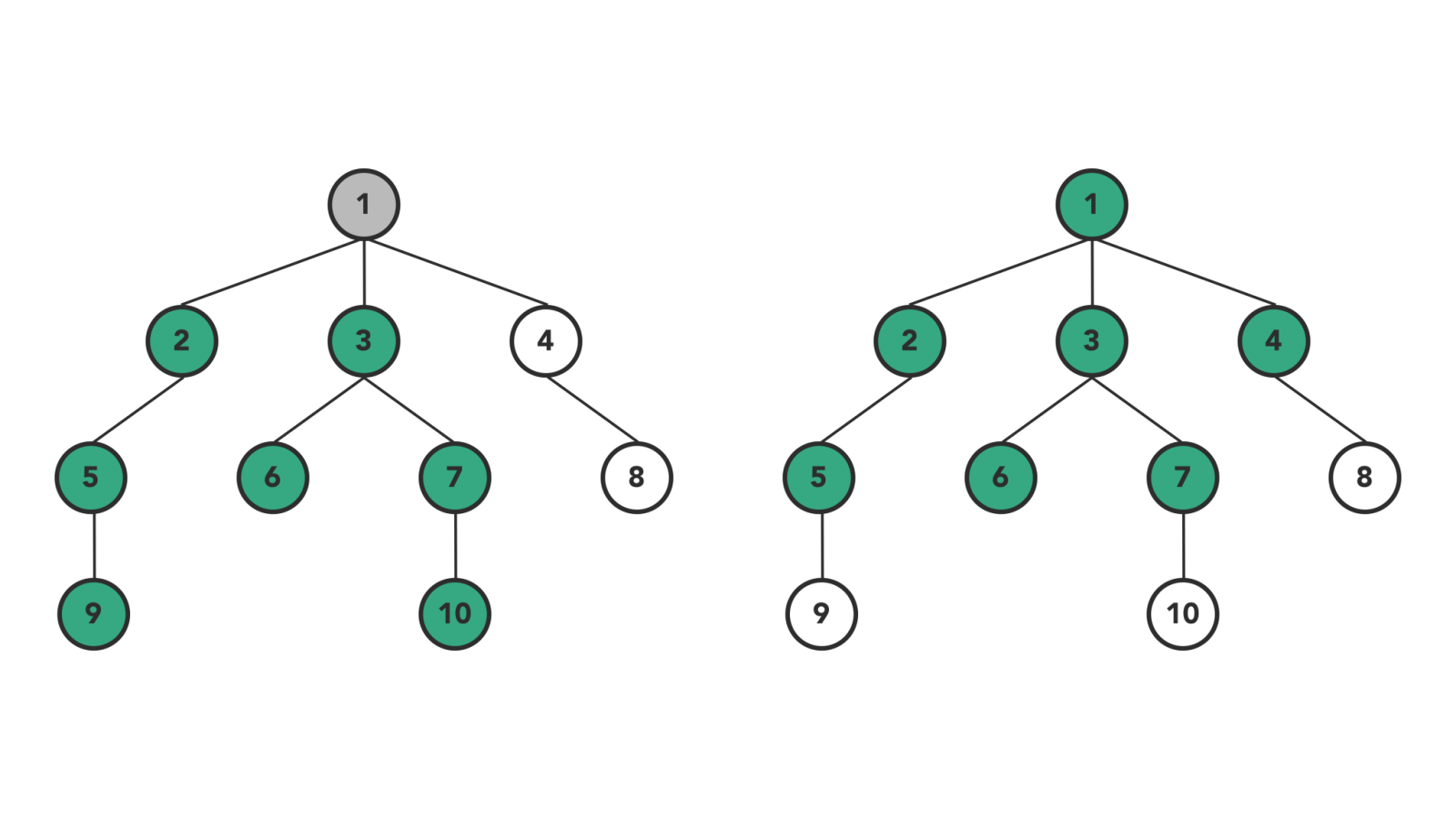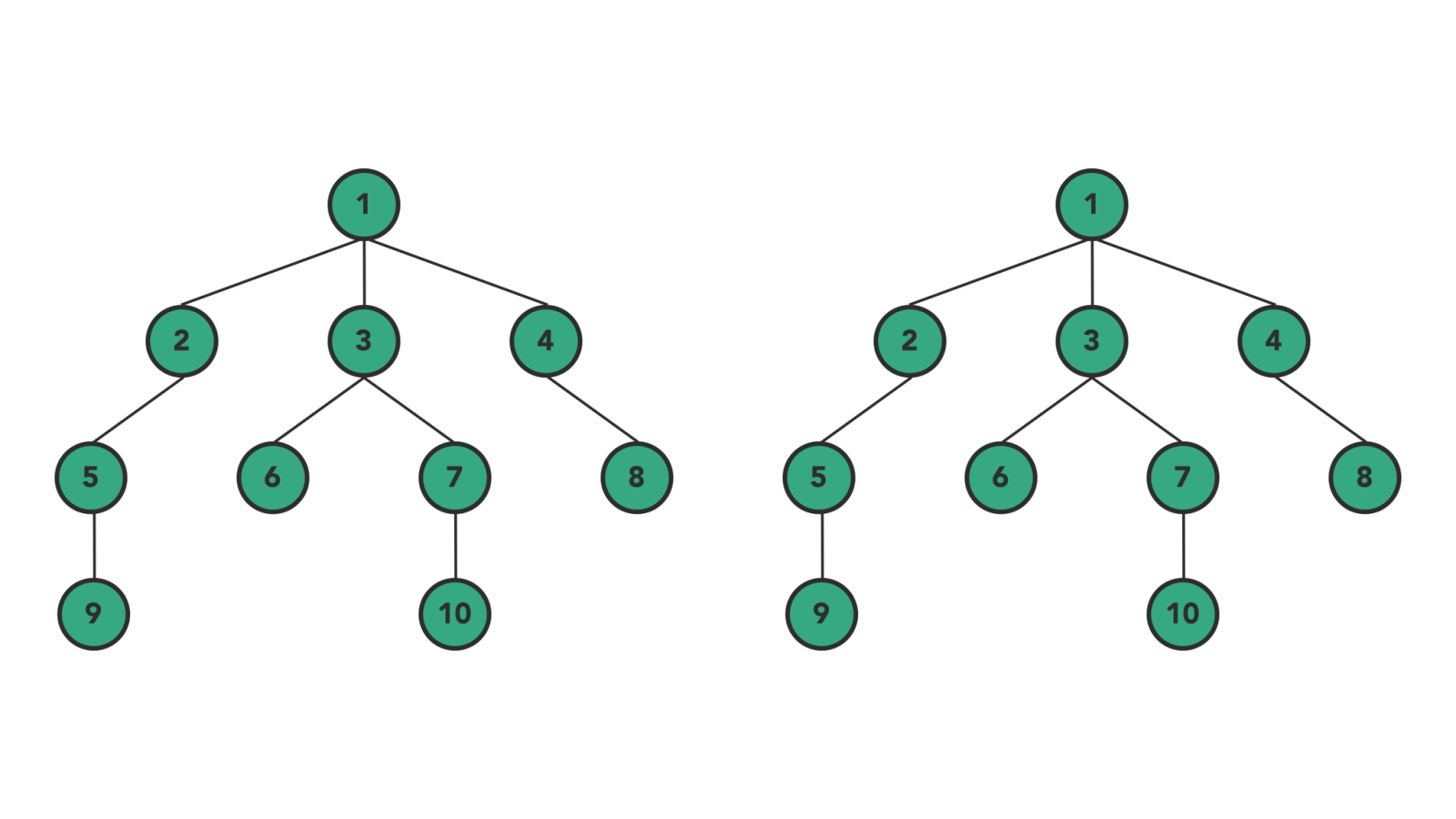
 #### DFS & BFS

### 树的遍历 - 先根遍历 - 后根遍历 - 层次遍历

### 先根遍历 - 访问根结点 - 按照从左到右的顺序先根遍历根的各棵子树

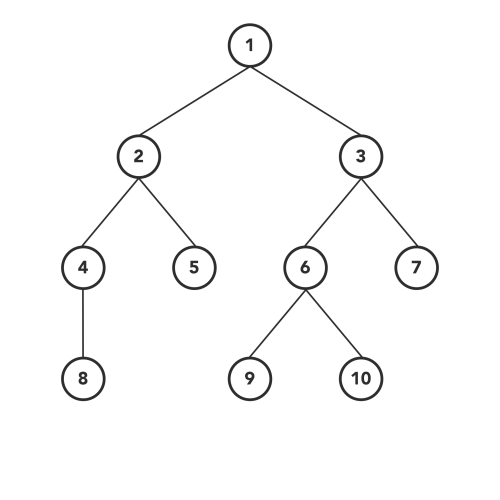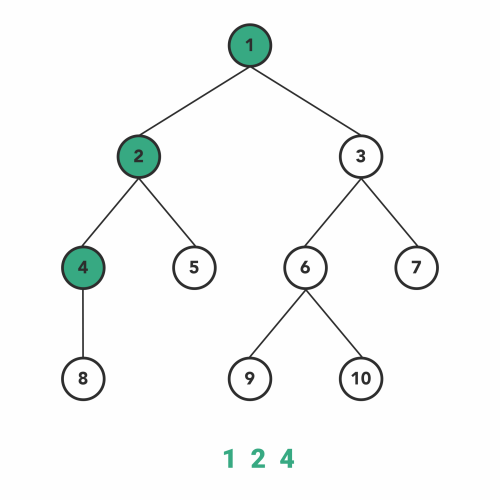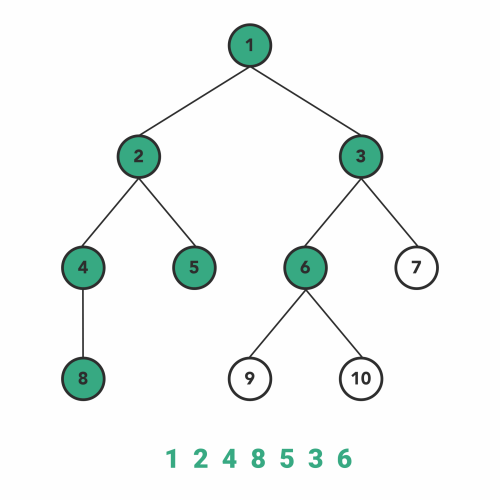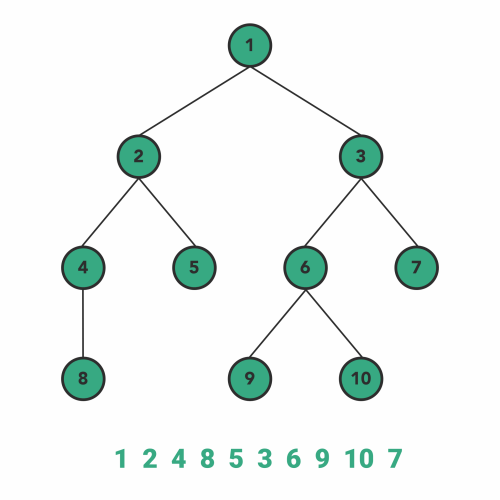
 #### PreOrder Traversal

### 后根遍历 - 按照从左到右的顺序后根遍历根的各棵子树 - 访问根结点

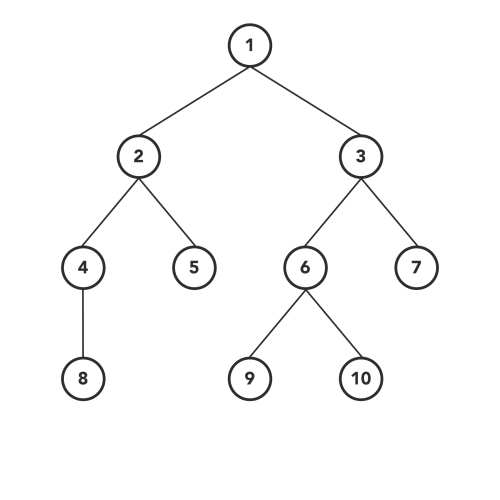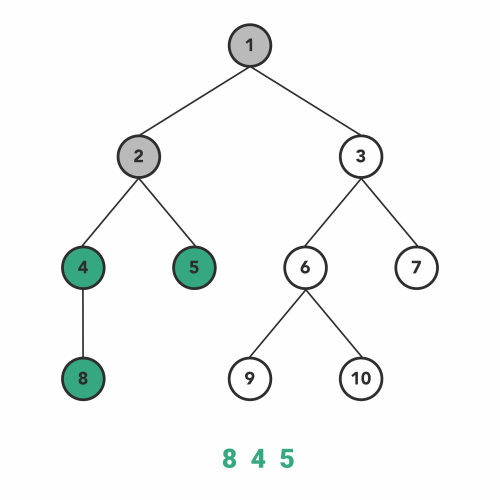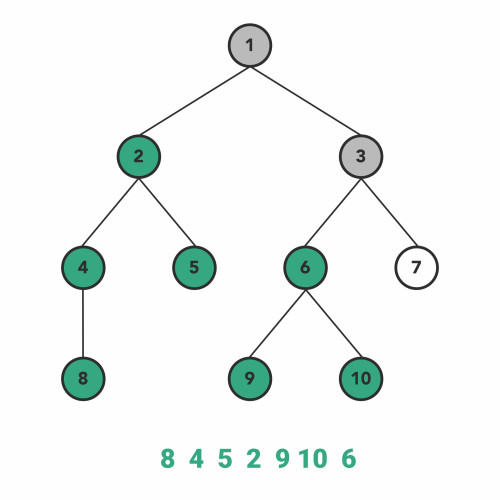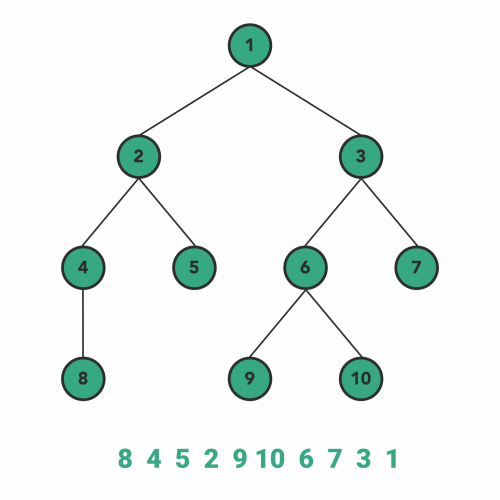
 #### PostOrder Traversal

### 层次遍历 - 从根节点开始 - 从上到下逐层遍历

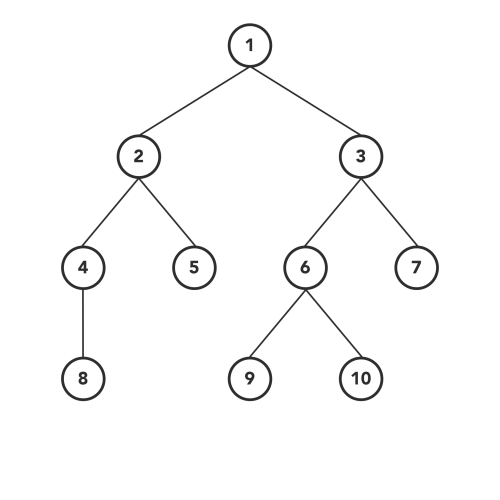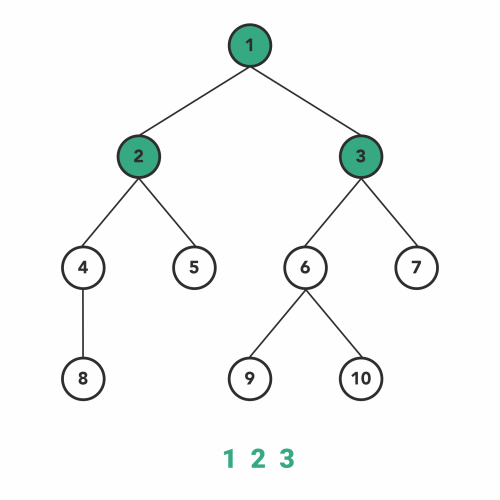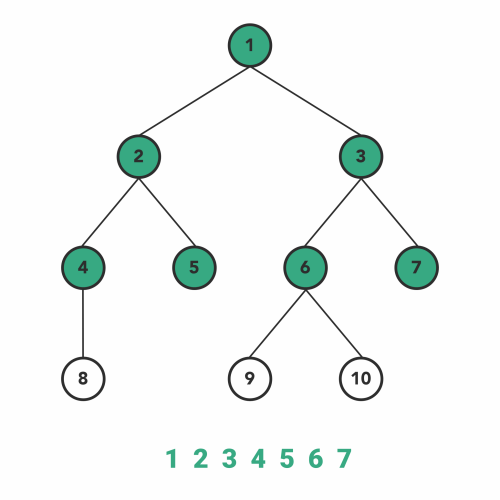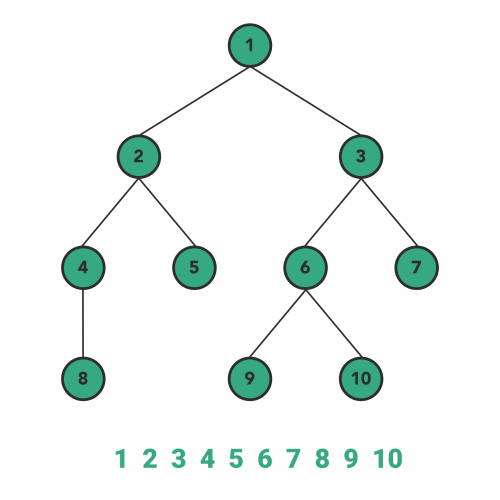
 #### Level Order Traversal

### 树的存储结构 - 双亲存储结构 - 孩子链存储结构 - 孩子兄弟链存储结构

### 双亲存储结构 - 顺序存储结构 - 每个结点都有一个伪指针 - 指向其双亲结点在数组中的位置 - 根节点指针为 $ -1 $

### 孩子链存储结构 - 每个结点包含数据和指针 - 指针指向所有孩子结点

### 孩子兄弟链存储结构 - 每个结点包含数据和两个指针 - 第一个指针指向第一个孩子结点 - 第二个指针指向下一个兄弟结点


### 10.1 树的基本概念 - 某个结点的度是 3, 这个结点具有多少个子树? - 哪种遍历方法会先访问根结点再递归访问左右子树? - 如果一棵树有 7 个结点, 最多可能有几个分支结点? - 在树的双亲存储结构中, 根节点的伪指针值是多少? - 一棵树所有结点的度数和为 20, 树有多少个结点? - 描述孩子兄弟链存储结构中的指针分配. ---- [ 9.7 递归](dbds-9-7.html#/overview) [| 练习 |](dbds-exec.html) [ 10.2 二叉树](dbds-10-2.html#/overview)