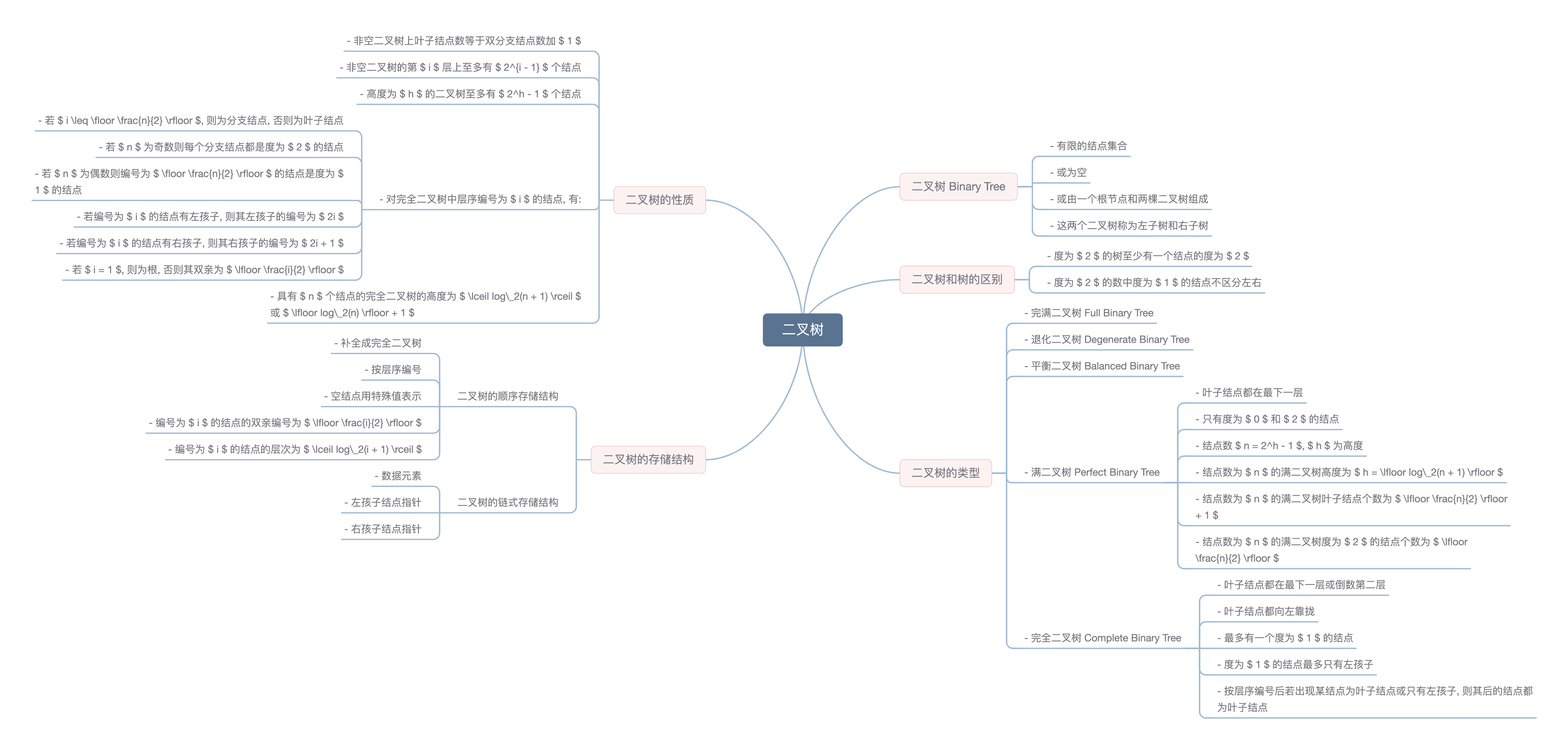
### 二叉树 Binary Tree - 有限的结点集合 - 或为空 - 或由一个根结点和两棵二叉树组成 - 这两个二叉树称为左子树和右子树

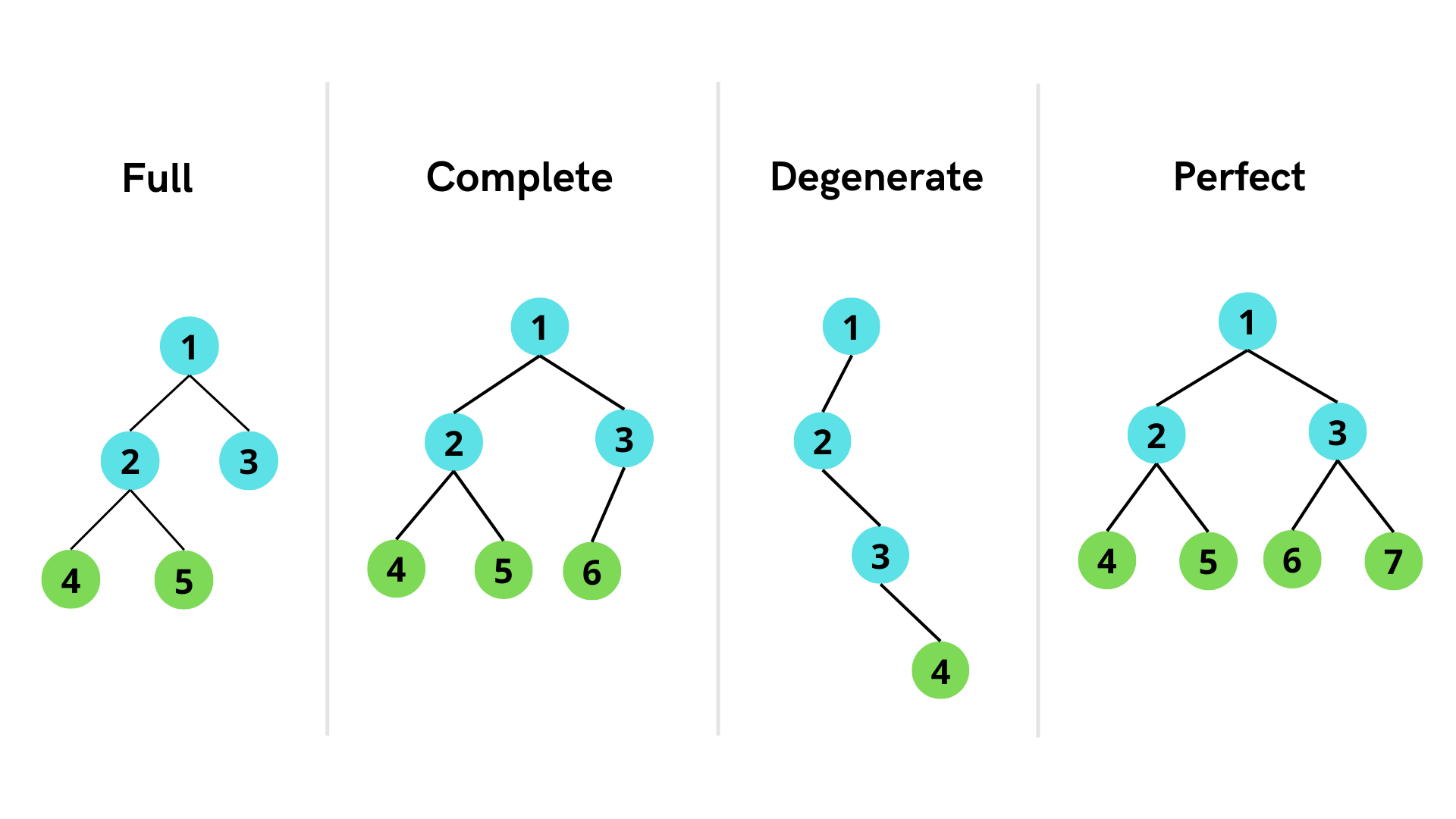
 #### Binary Tree

### 二叉树和树的区别 - 度为 $ 2 $ 的树至少有一个结点的度为 $ 2 $ - 度为 $ 2 $ 的树中度为 $ 1 $ 的结点不区分左右

### 二叉树的抽象数据结构 ADT BTree { 数据对象 $ D = \lbrace a\_i | 0 \leq i \leq n - 1, n \geq 0, a\_i \in ElemSet \rbrace $ 数据关系 $ r = \lbrace < a\_i, a\_j > | a\_i, a\_j \in D, 0 \leq i, j \leq n - 1 \rbrace $ 基本运算 void CreateBTree(string str) String toString() BTNode FindNode(x) int Height() }

### 二叉树的类型 - 完满二叉树 Full Binary Tree - 退化二叉树 Degenerate Binary Tree - 平衡二叉树 Balanced Binary Tree - 满二叉树 Perfect Binary Tree - 完全二叉树 Complete Binary Tree

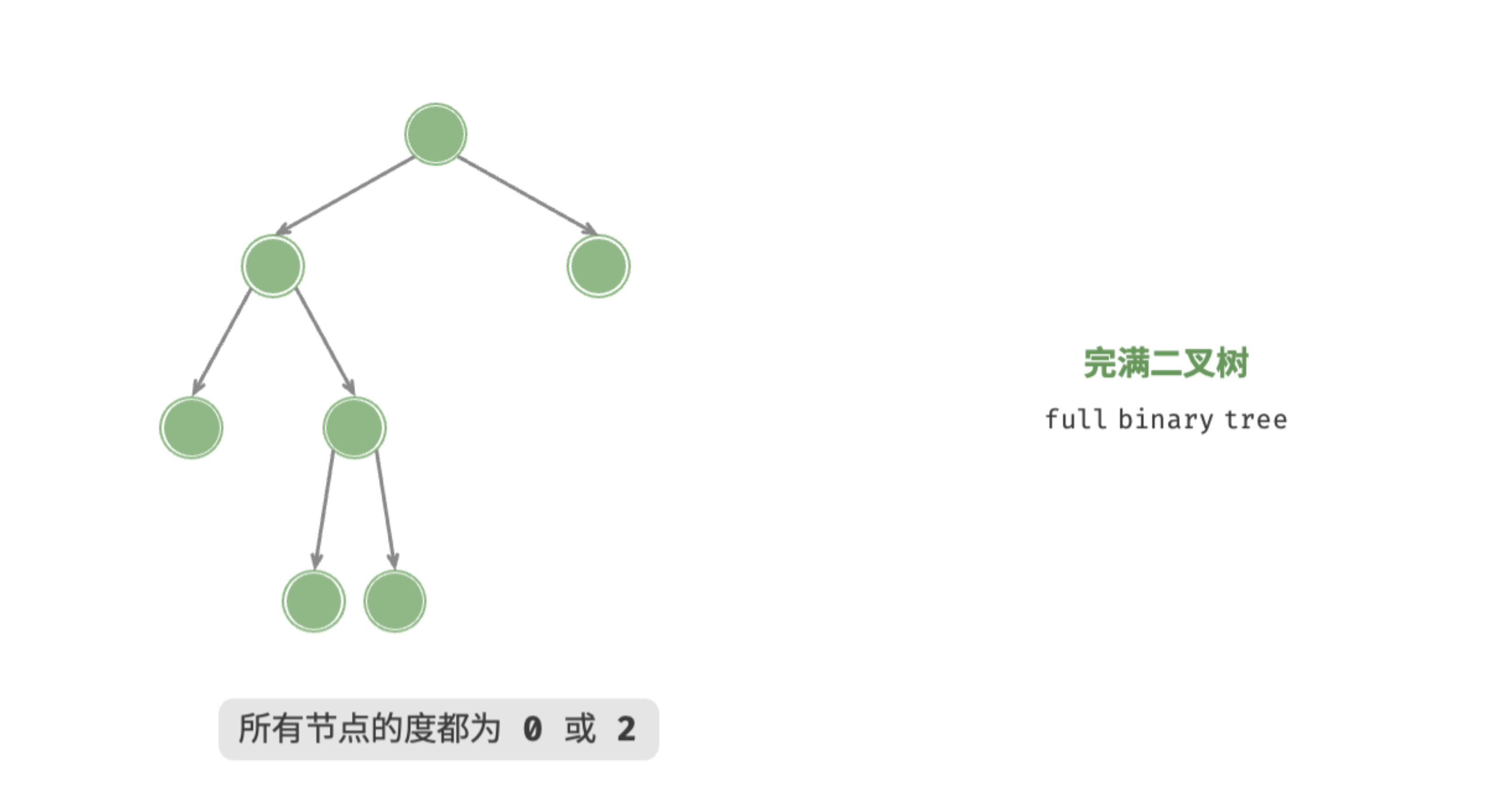
 #### Full Binary Tree

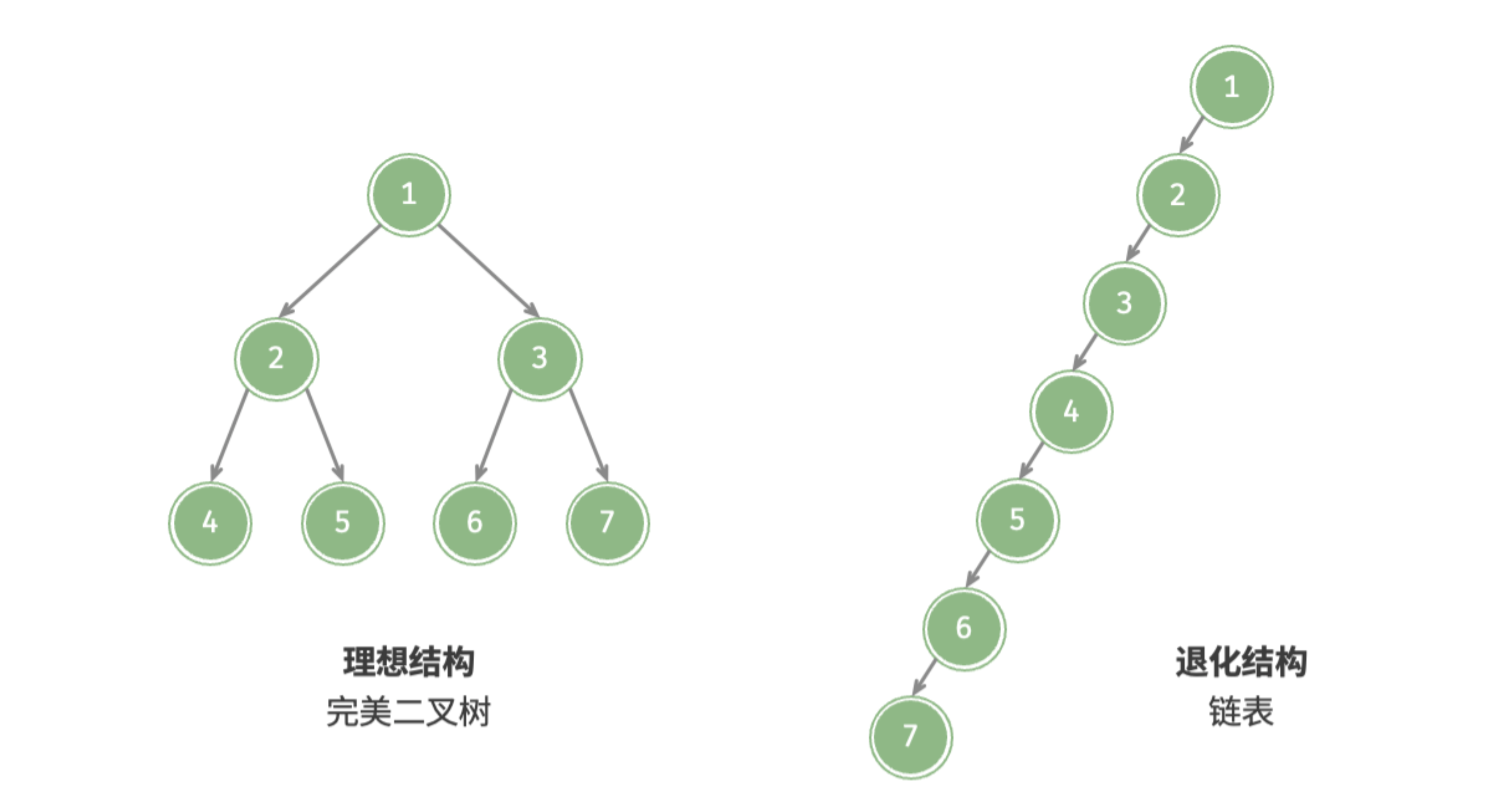
 #### Degenerate Binary Tree

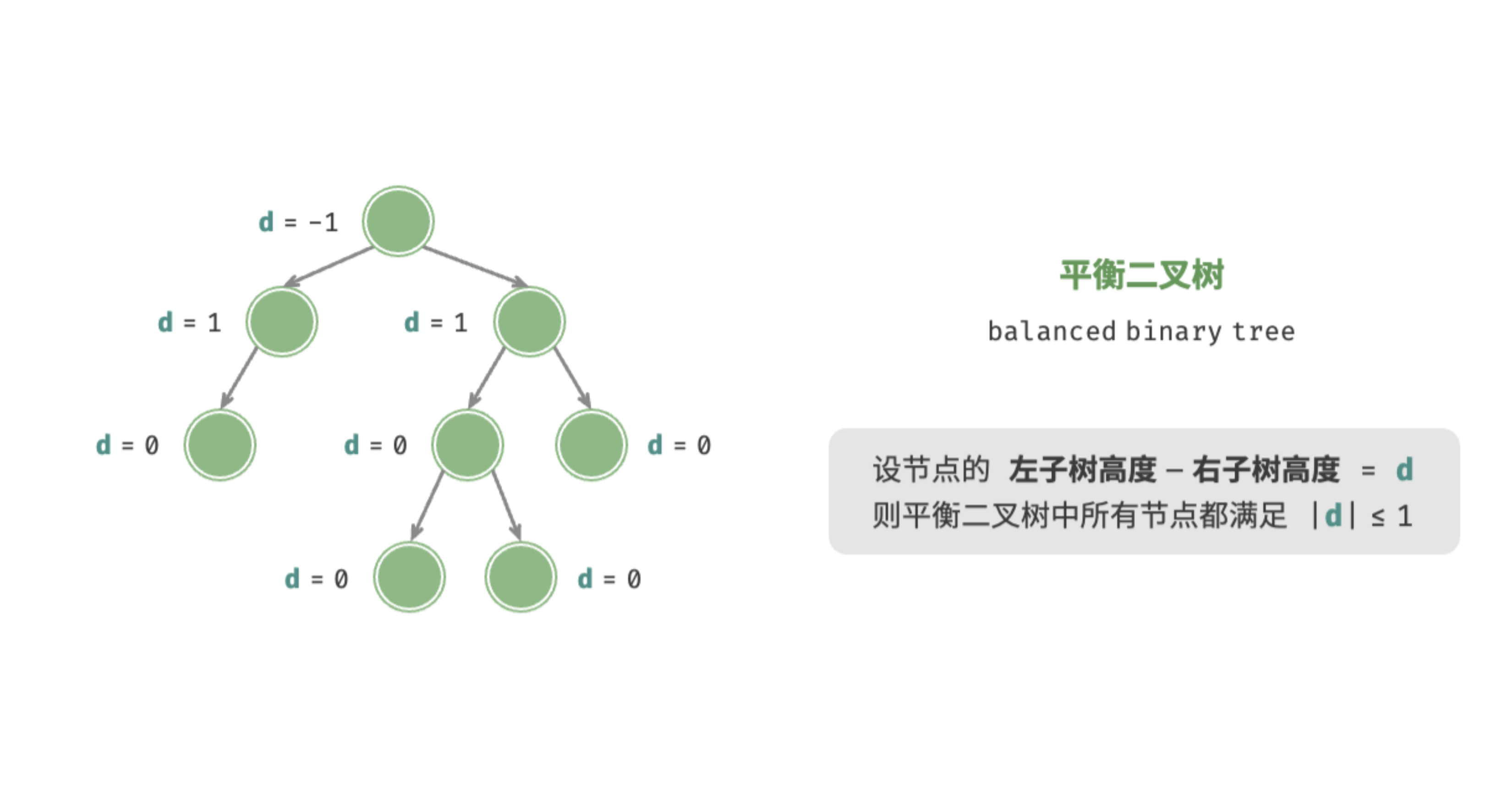
 #### Balanced Binary Tree

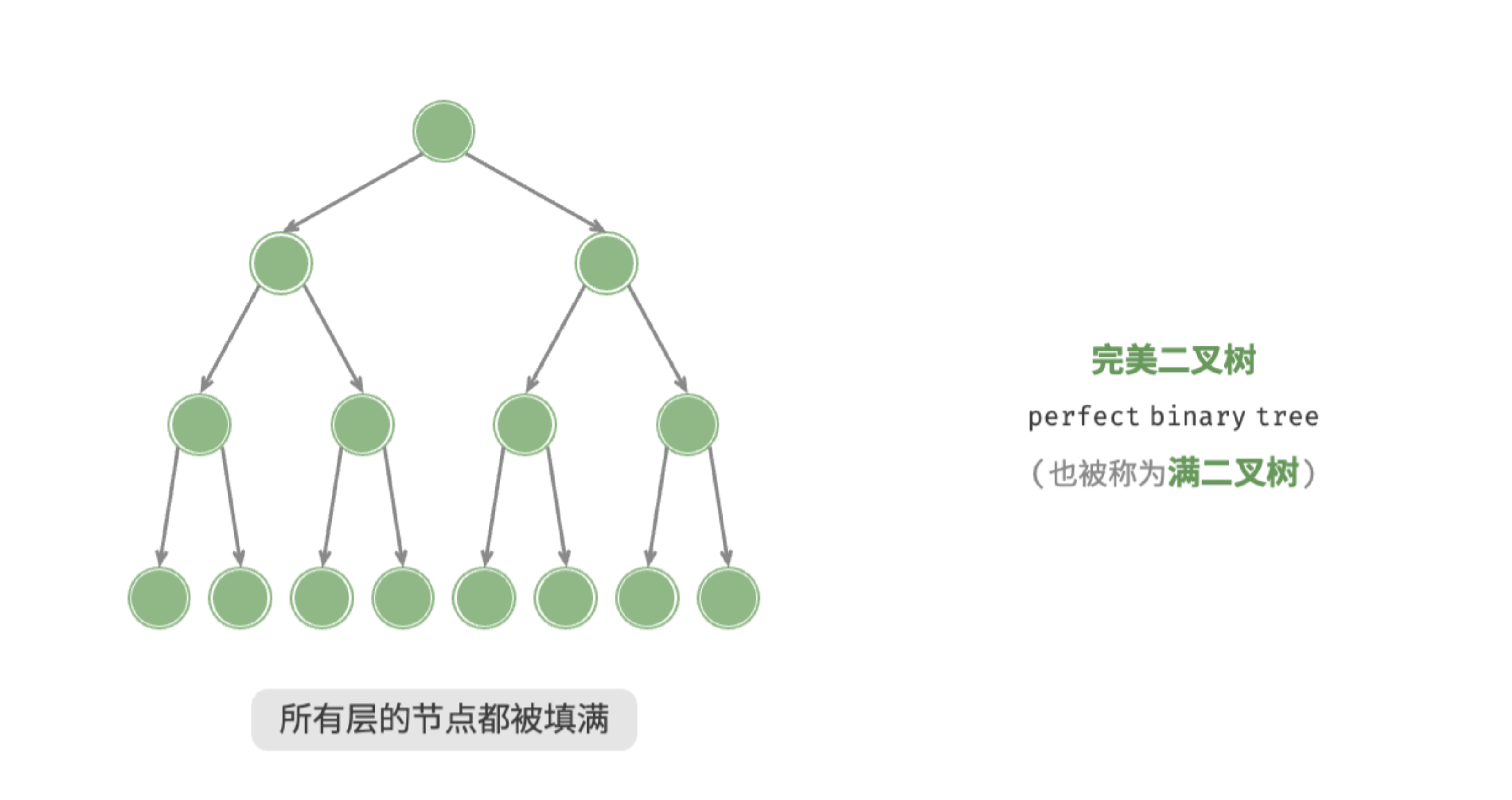
 #### Perfect Binary Tree

### 满二叉树 - 叶子结点都在最下一层 - 只有度为 $ 0 $ 和 $ 2 $ 的结点 - 结点数 $ n = 2^h - 1 $, $ h $ 为高度 - 结点数为 $ n $ 的满二叉树高度为 $ h = \lfloor log\_2(n + 1) \rfloor $ - 结点数为 $ n $ 的满二叉树叶子结点个数为 $ \lfloor \frac{n}{2} \rfloor + 1 $ - 结点数为 $ n $ 的满二叉树度为 $ 2 $ 的结点个数为 $ \lfloor \frac{n}{2} \rfloor $

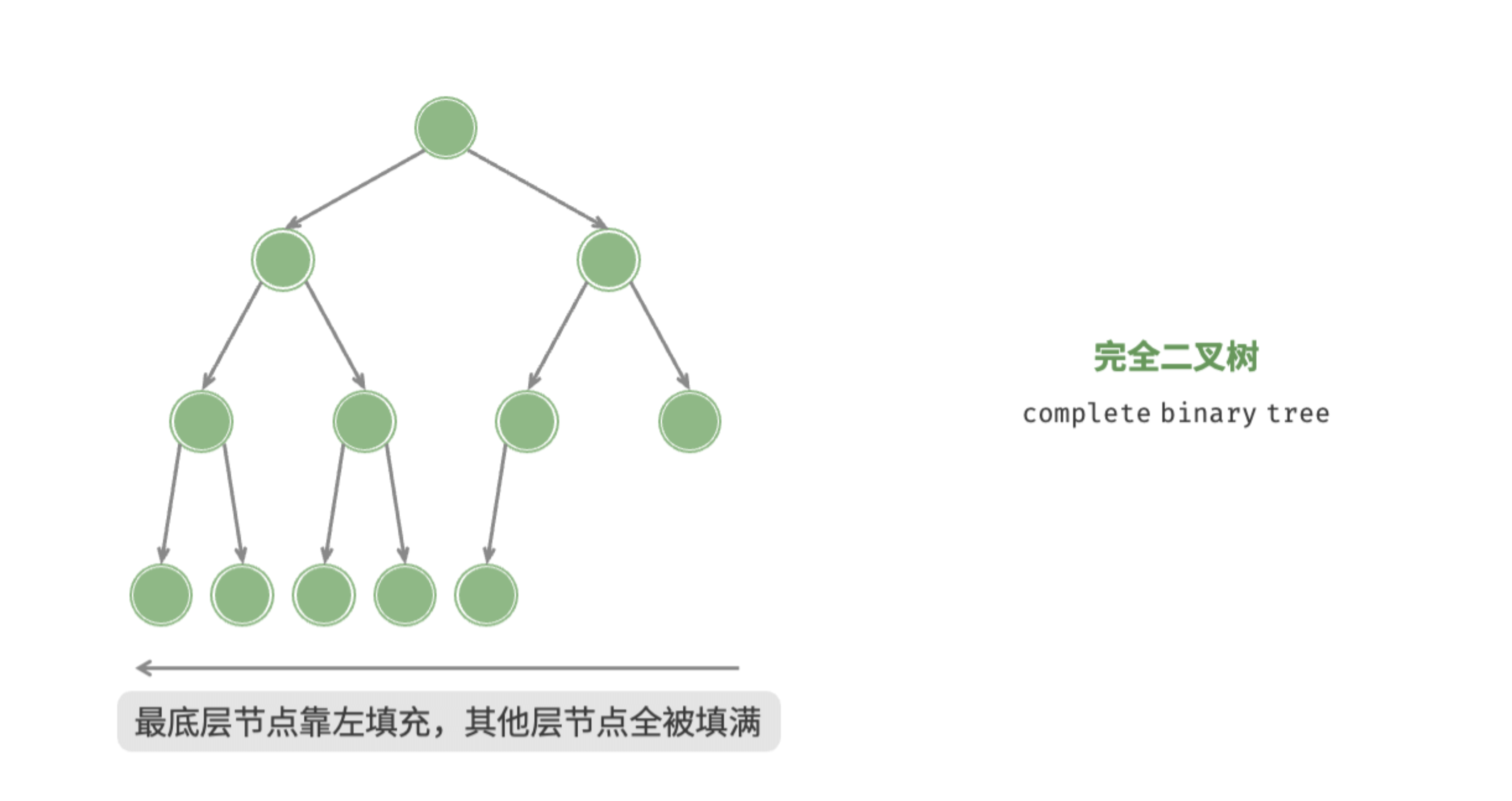
 #### Complete Binary Tree

### 完全二叉树 - 叶子结点都在最下一层或倒数第二层 - 叶子结点都向左靠拢 - 最多有一个度为 $ 1 $ 的结点 - 度为 $ 1 $ 的结点最多只有左孩子 - 按层序编号后, 若出现某结点为叶子结点或只有左孩子, 则其后的结点都为叶子结点

### 二叉树的性质 1 - 非空二叉树上叶子结点数等于双分支结点数加 $ 1 $

### 二叉树的性质 2 - 非空二叉树的第 $ i $ 层上至多有 $ 2^{i - 1} $ 个结点

### 二叉树的性质 3 - 高度为 $ h $ 的二叉树至多有 $ 2^h - 1 $ 个结点

### 二叉树的性质 4 - 对完全二叉树中层序编号为 $ i $ 的结点, 有: - 若 $ i \leq \lfloor \frac{n}{2} \rfloor $, 则为分支结点, 否则为叶子结点 - 若 $ n $ 为奇数则每个分支结点都是度为 $ 2 $ 的结点 - 若 $ n $ 为偶数则编号为 $ \lfloor \frac{n}{2} \rfloor $ 的结点是度为 $ 1 $ 的结点 - 若 $ i $ 结点有左孩子, 则其左孩子的编号为 $ 2i $ - 若 $ i $ 结点有右孩子, 则其右孩子的编号为 $ 2i + 1 $ - 若 $ i = 1 $, 则为根, 否则其双亲为 $ \lfloor \frac{i}{2} \rfloor $

### 二叉树的性质 5 - 具有 $ n $ 个结点的完全二叉树的高度为 $ \lceil log\_2(n + 1) \rceil $ 或 $ \lfloor log\_2(n) \rfloor + 1 $

## 10.3 二叉树的存储结构

### 二叉树的存储结构 - 顺序存储结构 - 链式存储结构

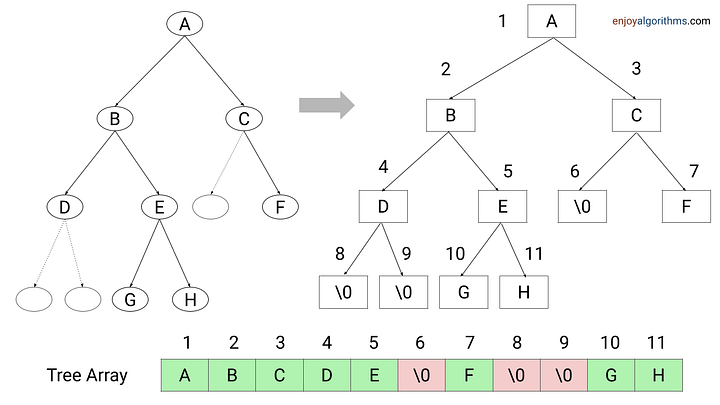
 #### Sequential Storage

### 二叉树的顺序存储结构 - 补全成完全二叉树 - 按层序编号 - 空结点用特殊值表示 - 编号为 $ i $ 的结点的双亲编号为 $ \lfloor \frac{i}{2} \rfloor $ - 编号为 $ i $ 的结点的层次为 $ \lceil log\_2(i + 1) \rceil $

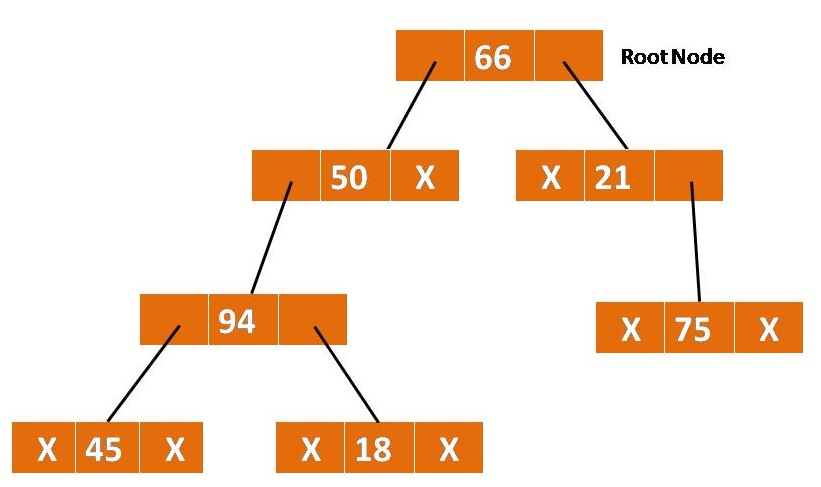
 #### Linked Storage

### 二叉树的链式存储结构 - 数据元素 - 左孩子结点指针 - 右孩子结点指针

### BTNode <E> class BTNode <E> { E data; BTNode lchild; BTNode rchild; public BTNode() { lchild = rchild = null; } public BTNode(E d) { data = d; lchild = rchild = null; } }


### 10.2 二叉树 - 有三个结点的二叉树至少有几个叶子结点? - 满二叉树与完全二叉树有何区别? - 在完全二叉树中, 如何找到一个结点的父结点? - 在二叉树的顺序存储结构中, 如何标识空结点? - 二叉链中某结点的左孩子指针为空, 说明了什么? ---- [ 10.1 树](dbds-10-1.html#/overview) [| 练习 |](dbds-exec.html) [ 10.4 二叉树的遍历](dbds-10-4.html#/overview)