### 集合运算 - 并 (Union) - 交 (Intersection) - 差 (Except) - 笛卡尔积 (Cartesian Product)

### 并运算 - 将两个关系的元组合并为一个关系 - 表示为 $R \cup S$ - $R \cup S = \lbrace t | t \in R \bigvee t \in S \rbrace$ - 运算的两个关系需要具有相同的属性集合

### 交运算 - 取两个关系的共有元组 - 表示为 $R \cap S$ - $R \cap S = \lbrace t | t \in R \bigwedge t \in S \rbrace$ - 运算的两个关系需要具有相同的属性集合

### 差运算 - 从一个关系中排除另一个关系中的元组 - 表示为 $R - S$ - $R - S = \lbrace t | t \in R \bigwedge t \notin S \rbrace$ - 运算的两个关系需要具有相同的属性集合

### 笛卡尔积运算 - 将两个关系的元组组合 - 表示为 $R \times S$ - $R \times S = \lbrace \overset{\frown} {t\_r t\_s} | t\_r \in R \bigwedge t\_s \in S \rbrace$ - 运算的两个关系可以具有不同的属性集合

### 关系运算 - 选择 (Selection) - 投影 (Projection) - 连接 (Join) - 除 (Division)

### 基本约定一 - 设关系模式为 $R(A\_1, A\_2, \cdots, A\_n)$, 它的一个关系设为 $R$ - $t \in R$ 表示 $t$ 是 $R$ 的一个元组 - $t[A\_i]$ 表示元组 $t$ 在属性 $A\_i$ 上的一个分量

### 基本约定二 - 若 $A = \lbrace A\_{i1}, A\_{i2}, \cdots, A\_{ik} \rbrace$, 其中 $A\_{i1}, A\_{i2}, \cdots, A\_{ik}$ 是 $A\_1, A\_2, \cdots, A\_n$ 中的一部分, 则 $A$ 称为属性列或属性组 - $t[A] = \lbrace t[A\_{i1}], t[A\_{i2}], \cdots, t[A\_{ik}] \rbrace$ 表示元组 $t$ 在属性集合 $A$ 上诸分量的集合 - $\bar{A}$ 表示属性集合 $A$ 的补集，即 $\bar{A}$ 为 $\lbrace A\_1, A\_2, \cdots, A\_n \rbrace$ 中去掉 $\lbrace t[A\_{i1}], t[A\_{i2}], \cdots, t[A\_{ik}] \rbrace$ 后剩余的属性组

### 基本约定三 - $R$ 为 $n$ 目关系, $S$ 为 $m$ 目关系, $t\_r \in R$, $t\_s \in S, \overset{\frown} {t\_r t\_s}$ 称为元组的连接 (concatenation) 或串接 - $\overset{\frown}{t\_r t\_s}$ 是一个 $n + m$ 目元组, 前 $n$ 个分量为 $R$ 中的一个 $n$ 元组, 后 $m$ 个分量为 $S$ 中的一个 $m$ 元组

### 基本约定四 - 给定一个关系 $R(X,Z), X$ 和 $Z$ 为属性组, 当 $t[X] = x$ 时, $x$ 在 $R$ 中的象集 (images set) 定义为 - $Z\_x = \lbrace t[Z] | t \in R, t[X] = x \rbrace$ - $Z\_x$ 是 $R$ 中所有满足 $t[X] = x$ 的元组在属性组 $Z$ 上的分量的集合

### 选择 - 从关系中选择满足特定条件的元组 - 表示为 $\sigma_{condition}(R)$ - $\sigma$ 是选择运算符 - $condition$ 是谓词条件 - $R$ 是待选择的关系 - $\sigma\_F(R)$ 表示选择满足条件 $F(t)$ 为真的元组 $t$ - 选择是行运算

### 投影 - 从关系中选择指定的属性列 - 表示为 $\Pi_{A\_1, A\_2, \cdots, A\_n}(R)$ - $\Pi$ 是投影运算符 - $A\_1, A\_2, \cdots, A\_n$ 是待投影的属性列 - $R$ 是待投影的关系 - 投影是列运算

### 连接 - 组合两个关系中的元组 - 基于某个属性的值匹配 - 表示为 $R \mathop{\bowtie}\limits_{A\theta B}S$ - $\mathop{\bowtie}\limits_{A\theta B}$ 是连接运算符 - $R$ 和 $S$ 是待连接的关系 - 也称为 $\theta$ 连接, $\theta$ 是连接条件 - 连接运算从 $R$ 和 $S$ 的笛卡儿积 $R \times S$ 中选取 $R$ 关系在 $A$ 属性组上的值与 $S$ 关系在 $B$ 属性组上的值满足比较运算符 $\theta$ 的条件的元组

### 等值连接 - 基于指定的等值条件连接两个关系 - 表示为 $R \mathop{\bowtie}\limits_{A = B}S$

### 自然连接 - 一种特殊的等值连接 - 自动匹配具有相同属性名称的属性组 - 删除重复的属性列 - 记作 $R \bowtie S$

### 除 - 从关系 $R$ 中选择满足某个条件的元组 - 并删除与关系 $S$ 中对应属性的值不匹配的元组 - 表示为 $R \div S$ - $\div$ 是除运算符 - $R$ 和 $S$ 是待操作的关系


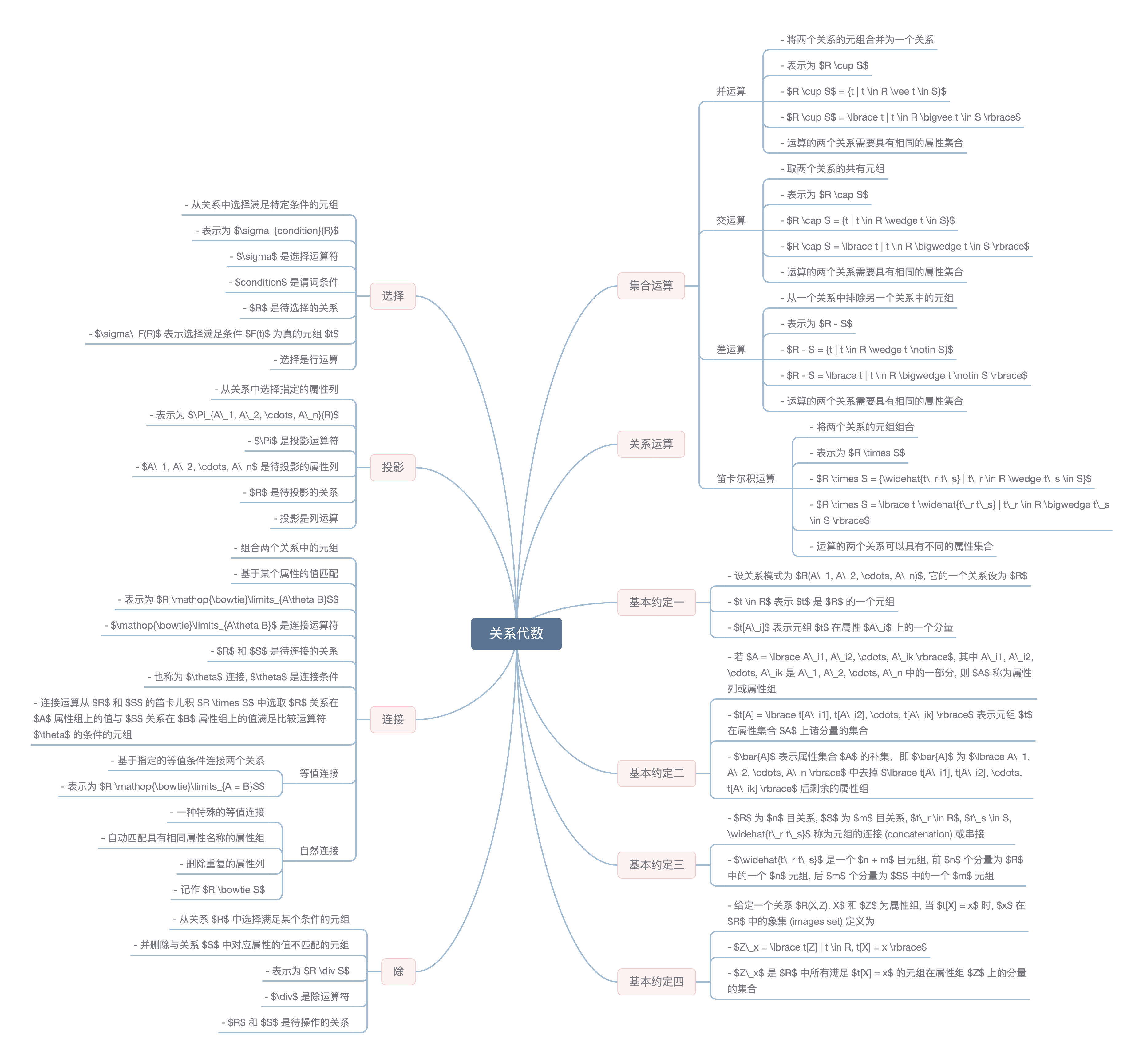
### 2.4 关系代数 - 交运算需要的两个关系有什么特别要求? - 笛卡尔积运算的关系是否需要有相同属性集合? - 请解释元组的连接. - 什么是选择运算? - 连接运算如何工作? ---- [ 2.3 关系的完整性](dbds-2-3.html#/overview) [| 练习 |](dbds-exec.html) [ 3.1 SQL 概述](dbds-3-1.html#/overview)