### 算法设计的要求
- 正确性
- 可使用性
- 可读性
- 健壮性
- 高效率与低存储量
### 正确性
- 能够正确地执行预先规定的功能和性能要求
- 是最重要也是最基本的标准
### 可使用性
- 能够很方便地使用
- 也叫用户友好性
### 可读性
- 应该易于使人理解
- 逻辑清晰, 简单和结构化
### 健壮性
- 具有好的容错性
- 提供异常处理
- 能够对不合理的数据进行检查
- 不经常出现异常中断或死机
### 高效率与低存储量
- 算法的效率主要指算法执行时间
- 执行时间短的算法效率高
- 存储量指执行过程中所需最大存储空间
### 算法时间性能分析
- 事后统计法
- 事前估算法
### 事后统计法
- 统计程序执行时间
- 与很多因素有关
### 事前估算法
- 顺序结构
- 分支结构
- 循环结构
- 原操作
- 执行时间由原操作的执行次数来计量
### 算法频度
- 所有原操作的执行次数之和
- 用 $T(n)$ 表示
### 方阵相加
void matrixadd(int[][] A, int[][] B, int[][] C, int n) {
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
C[i][j] = A[i][j] + B[i][j];
}
$T(n) = n+1+n(n+1)+n^2$
$T(n) = 2n^2+2n+1 = O(n^2)$
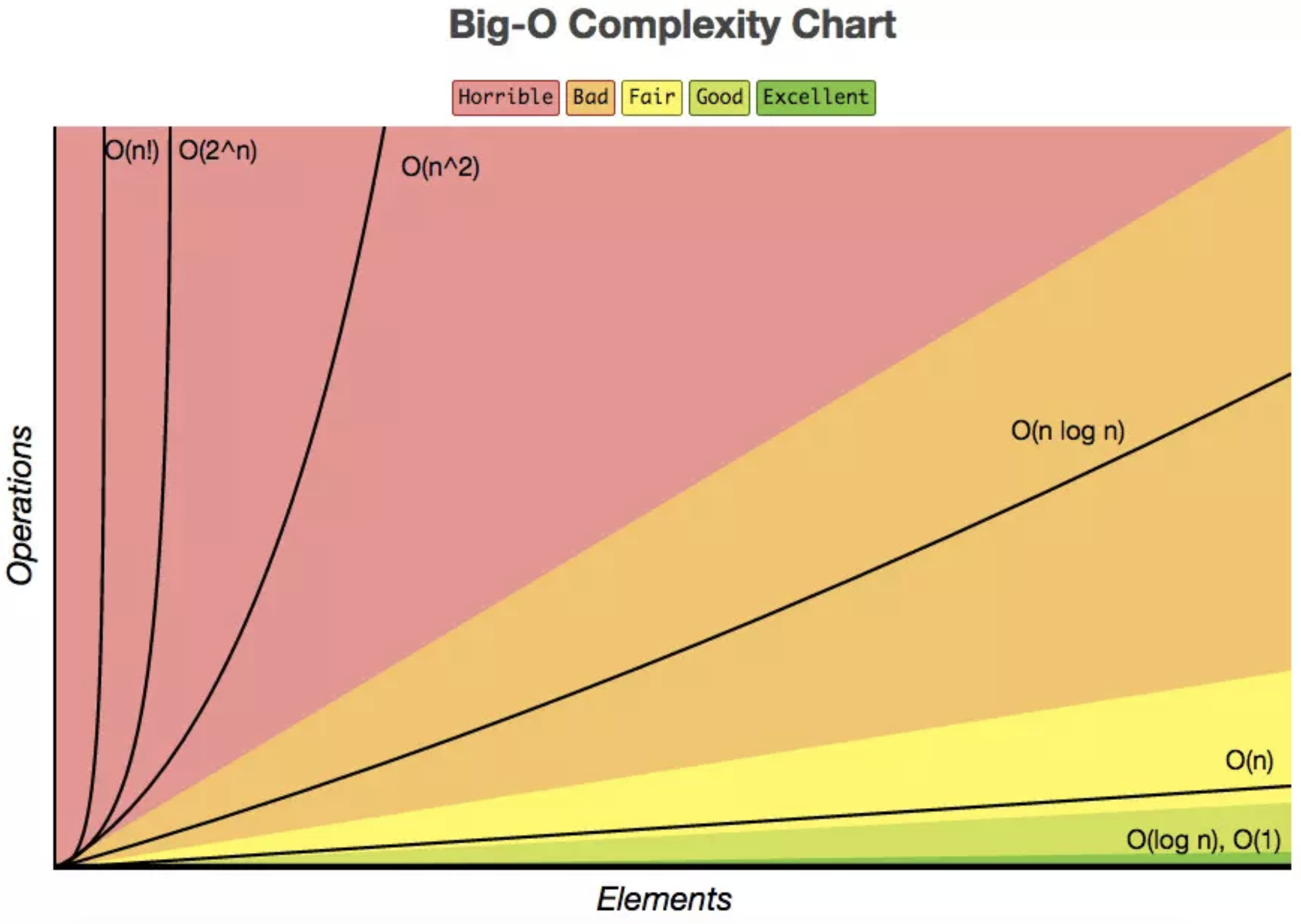
### 算法时间复杂度
- $T(n)$ 的数量级, 即 $T(n) = O(f(n))$
- 存在正常量 $C$ 和 $n\_0$
- 使得当 $\lim\limits_{n \to n\_0} \frac{\lvert T(n) \rvert}{\lvert f(n) \rvert} \leq C \ne 0$
### 算法复杂度
void fun(int n){
int s = 0;
for (i = 0; i < n; i++)
for (j = 0; j < i; j++)
for (int k = 0; k < j; k++)
s++;
return s;
}
$$
\begin{eqnarray*}
T(n) &=& \sum\limits_{i=0}^n \sum\limits_{j=0}^i \sum\limits_{k=0}^{j-1} 1 \\\
&=& \sum\limits_{i=0}^n \sum\limits_{j=0}^i (j-1-0+1) = \sum\limits_{i=0}^n \sum\limits_{j=0}^i j \\\
&=& \sum\limits_{i=0}^n \frac{i(i+1)}{2} = \frac{1}{2}(\sum\limits_{i=0}^n i^2 + \sum\limits_{i=0}^n i) \\\
&=& \frac{2n^3 + 6n^2 + 4n}{12} = O(n^3)
\end{eqnarray*}
$$
#### Big-O Complexity Chart
### 算法的空间复杂度
- 算法的空间复杂度是指算法需要消耗的内存空间
- $S(n) = O(g(n))$
### 8.3 算法分析
- 算法设计的要求有哪些?
- 为什么在算法设计中可读性很重要?
- 健壮性在算法设计中的作用是什么?
- 请解释高效率与低存储量的含义.
- 算法时间性能分析有哪两种方法?
- 事前估算法中, 如何计量算法执行时间?
- 什么是算法空间复杂度?
----
[ 8.2 算法及其描述](dbds-8-2.html#/overview)
[| 练习 |](dbds-exec.html)
[ 8.4 数据结构的目标](dbds-8-4.html#/overview)
黑公网安备23010302001726号