### 算法的评价标准
- 占用资源越少就越好
- 时间复杂度分析
- 空间复杂度分析
### 存储结构对算法的影响
- 存储能力
- 与算法的适应性
### 抽象数据类型的实现
- Set
- TwoSet
### Set
class Set<E>
{
final int MaxSize=100;
E[] data;
int size;
public Set()
{ data = (E[])new Object[MaxSize];
size=0;
}
}
### Set.getsize()
public int getsize()
{
return size;
}
- 时间复杂度是?
### Set.get()
public E get(int i)
{
return (E)data[i];
}
- 时间复杂度是?
### Set.IsIn()
public boolean IsIn(E e)
{
for (int i=0;i<size;i++)
if (data[i]==e)
return true;
return false;
}
- 时间复杂度是?
### Set.add()
public boolean add(E e)
{
if (IsIn(e))
return false;
else
{
data[size]=e;
size++;
return true;
}
}
- 时间复杂度是?
### Set.delete()
public boolean delete(E e)
{
int i=0;
while (i<size && data[i]!=e) i++;
if (i>=size) return false;
for (int j=i+1;j<size;j++)
data[j-1]=data[j];
size--;
return true;
}
- 时间复杂度是?
### Set.display()
public void display()
{
for (int i=0;i<size;i++)
{
if (i==0)
System.out.print(data[i]);
else
System.out.print(" "+data[i]);
}
System.out.println();
}
- 时间复杂度是?
### TwoSet.Union()
{
public Set<E> Union(Set<E> s1,Set<E> s2)
{
Set<E> s3=new Set<E>();
for (int i=0;i<s1.getsize();i++)
s3.add(s1.get(i));
for (int i=0;i<s2.getsize();i++)
if (!s1.IsIn(s2.get(i)))
s3.add(s2.get(i));
return s3;
}
- 时间复杂度是?
### TwoSet.Intersection()
public Set<E> Intersection(Set<E> s1,Set<E> s2)
{
Set<E> s3=new Set<E>();
for (int i=0;i<s1.getsize();i++)
if (s2.IsIn(s1.get(i)))
s3.add(s1.get(i));
return s3;
}
- 时间复杂度是?
### TwoSet.Difference()
public Set<E> Difference(Set<E> s1,Set<E> s2)
{
Set<E> s3=new Set<E>();
for (int i=0;i<s1.getsize();i++)
if (!s2.IsIn(s1.get(i)))
s3.add(s1.get(i));
return s3;
}
- 时间复杂度是?
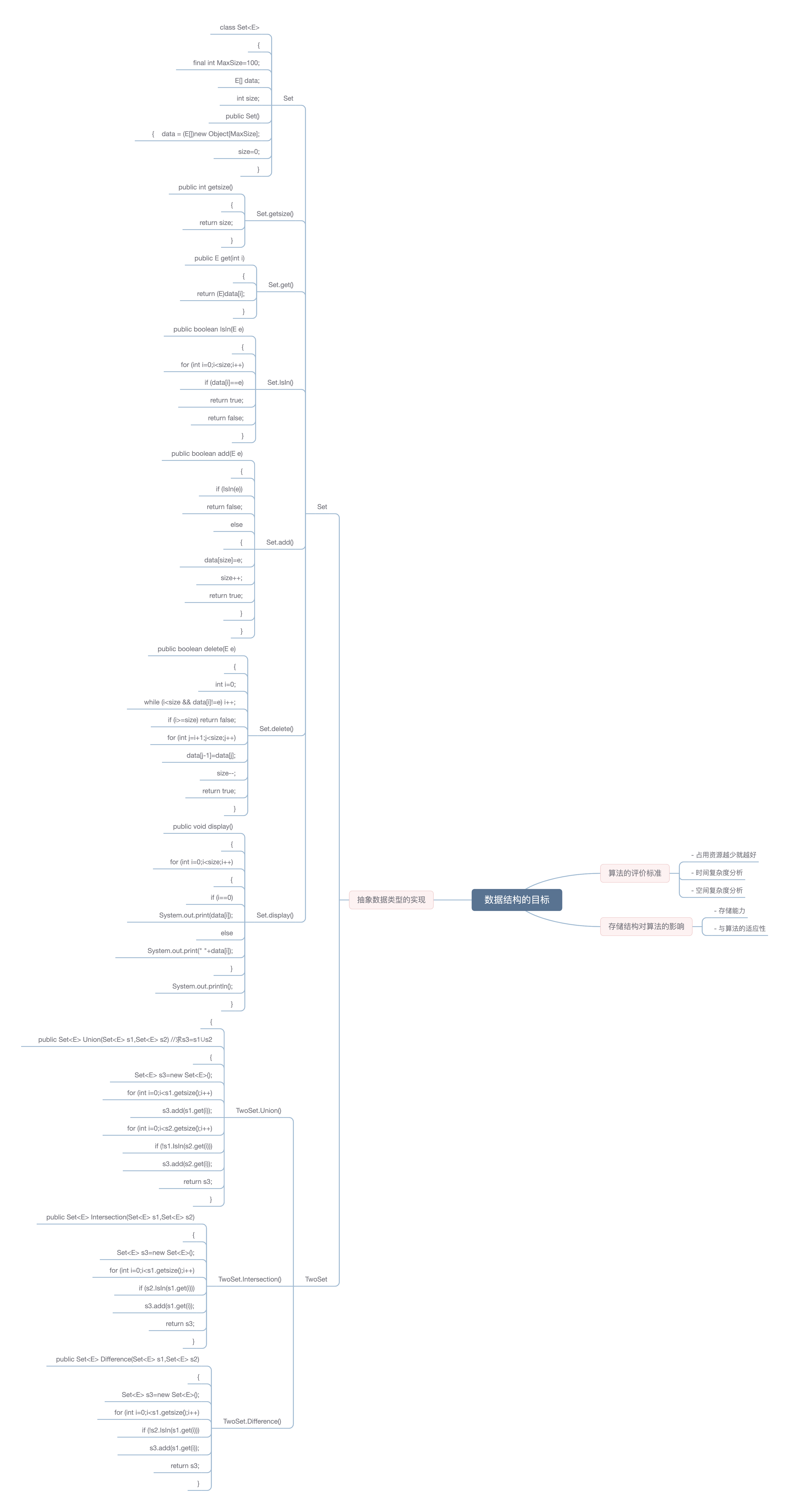
### 8.4 数据结构的目标
- 什么是算法的评价标准?
- 存储结构对算法有哪些影响?
- Set 类是什么抽象数据类型?
- Set 类中的 add() 方法的作用是什么?
- Set 类中的 display() 方法的作用是什么?
----
[ 8.3 算法分析](dbds-8-3.html#/overview)
[| 练习 |](dbds-exec.html)
[ 9.1 线性表的定义](dbds-9-1.html#/overview)