### 线性表 List - 数据元素排列像一条线 - 所有数据元素类型相同 - 由有限个数据元素组成 - 每个数据元素有唯一序号

### 线性表的逻辑结构 - $ L = (a\_0, a\_1, a\_2, \dots, a\_i, \dots, a\_{n-1}) $

### 线性表的构成 - 开始元素 (首元素) - 终端元素 (尾元素) - 前驱元素 - 后继元素

### 线性表的抽象数据类型 ADT List { 数据对象: $$ D = \lbrace a\_i | 0 \leq i \leq n-1, n \geq 0, a\_i 为 E 类型 \rbrace $$ 数据关系: $$ r = \lbrace <a\_{i}, a\_{i+1}> | a\_i, a\_{i+1} \in D, i = 0, \dots, n-2 \rbrace $$

ADT List 基本运算: void CreateList(E[] a) void Add(E e) int size() void Setsize(int nlen) E GetElem(int i) void SetElem(int i, E e) int GetNo(E e) void swap(int i, int j) void Insert(int i, E e) void Delete(int i) String toString() } ADT List

### 顺序存储结构 - 把元素按照逻辑顺序依次存放在一组地址连续的存储单元里 - 顺序表 - 静态分配 - 动态分配

### 动态分配 - 使用数组存储 `data` - 定义数组大小 `capacity` - 随时记录 `size` - $ size \leq capacity $

### SqlistClass<E> public class SqlistClass<E> { final int initcapacity = 10; public E[] data; public int size; private int capacity; public SqlistClass() { data = (E[]) new Object[init capacity]; capacity = initcapacity; size = 0; }

### updatecapacity(int newcapacity) private void updatecapacity(int newcapacity) { E[] newdata = (E[]) new Object[newcapacity]; for (int i = 0; i < size; i++) newdata[i] = data[i]; capacity = newcapacity; data = newdata; }

### CreateList(E[] a) public void CreateList(E[] a) { int i,k = 0; for(i = 0; i < a.length; i++) {if (size == capacity) updatecapacity(2 * size); data[k] = a[i]; k++; } size = k; } - 时间复杂度 $ \mathcal{O}(n) $

### Add(E e) public void Add[E e] { if (size == capacity) updatecapacity(2 * size); data[size] = e; size++; } - 时间复杂度 $ \mathcal{O}(1) $

### size() public int size() { return size; } - 时间复杂度 $ \mathcal{O}(1) $

### Setsize(int nlen) public void Setsize(int nlen) { if (nlen < 0 || nlen > size) throw new IllegalArgumentException( "设置长度: n 不在有效范围内"); size = nlen; } - 时间复杂度 $ \mathcal{O}(1) $

### GetElem(int i) public E GetElem(int i) { if (i < 0 || i > size - 1) throw new IllegalArgumentException( "取元素: i 不在有效范围内"); return (E)data[i]; } - 时间复杂度 $ \mathcal{O}(1) $

### SetElem(int i, E e) public void SetElem(int i, E e) { if (i < 0 || i > size - 1) throw new IllegalArgumentException( "设置元素: i 不在有效范围内"); data[i] = e; } - 时间复杂度 $ \mathcal{O}(1) $

### GetNo(E e) public int GetNo(E e) { int i = 0; while(i < size && !data[i].equals(e)) i++; if(i >= size) return -1; else return i; } - 时间复杂度 $ \mathcal{O}(n) $

### swap(int i, int j) public void swap(int i, int j) { E temp = data[i]; data[i] = data[j]; data[j] = temp; } - 时间复杂度 $ \mathcal{O}(1) $

### Insert(int i, E e) public void Insert(int i, E e) { if (i < 0 || i > size) throw new IllegalArgumentException( "插入元素: i 不在有效范围内"); if (size == capacity) updatecapacity(2 * size); for (int j = size ; j > i; j--) data[j] = data[j -1]; data[i] = e; size++; } - 时间复杂度 $ \mathcal{O}(n) $

### Delete(int i) public void Delete(int i) { if (i < 0 || i > size - 1) throw new IllegalArgumentException( "删除元素: i 不在有效范围内"); for (int j = i; j < size - 1; j++) data[j] = data[j + 1]; size--; if(capacity > initcapacity && size == capacity / 4) updatecapacity(capacity / 2); } - 时间复杂度 $ \mathcal{O}(n) $

### toString() public String toString() { String ans = ""; for (int i = 0; i < size; i++) ans += data[i].toString() + " "; return ans; } - 时间复杂度 $ \mathcal{O}(n) $


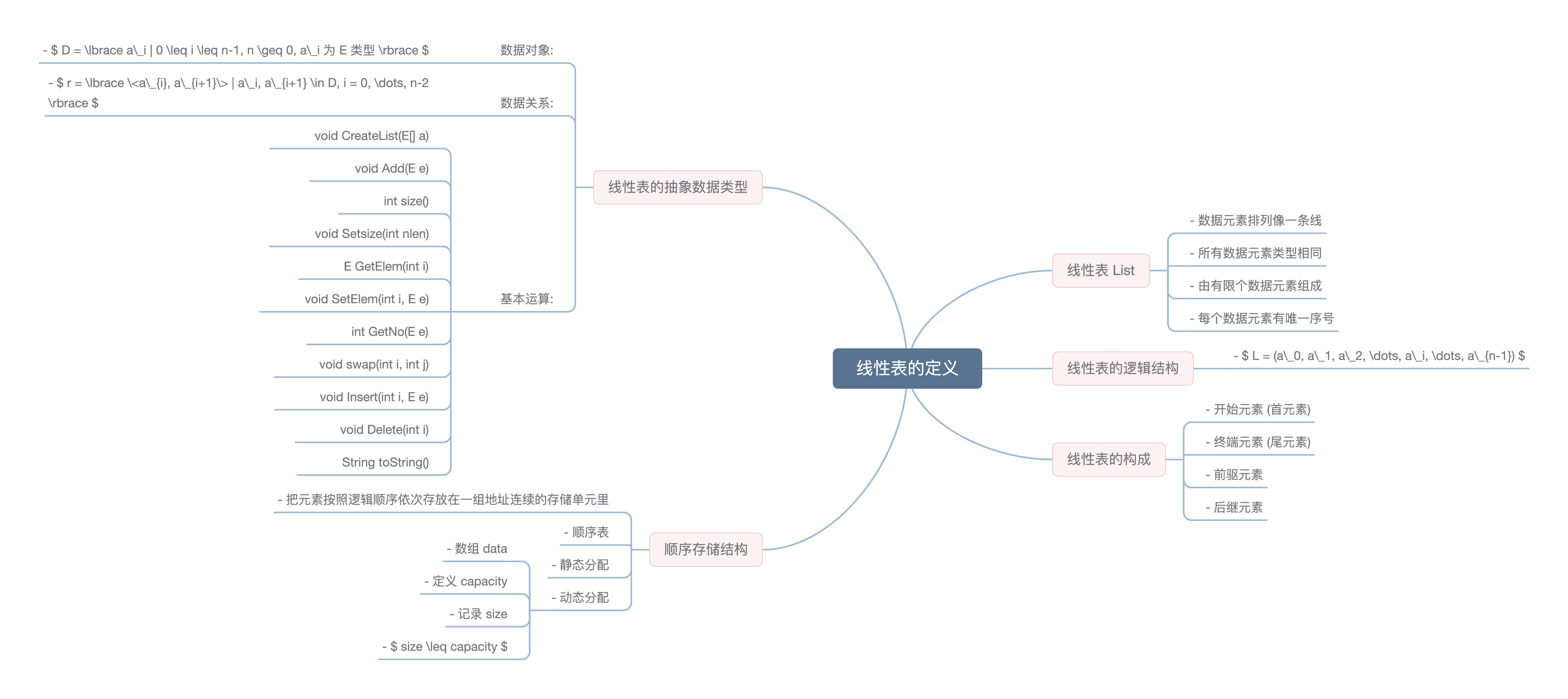
### 9.1 线性表的定义 - 线性表的数据元素有什么特点? - 在线性表中, 如何定义前驱元素和后继元素? - Add(E e) 和 Insert(int i, E e) 有什么区别? - 什么是静态分配和动态分配? - 在顺序存储结构中, capacity 和 size 之间应满足什么条件? ---- [ 8.4 数据结构的目标](dbds-8-4.html#/overview) [| 练习 |](dbds-exec.html) [ 9.3 线性表的链式存储结构](dbds-9-3.html#/overview)