### 栈的定义
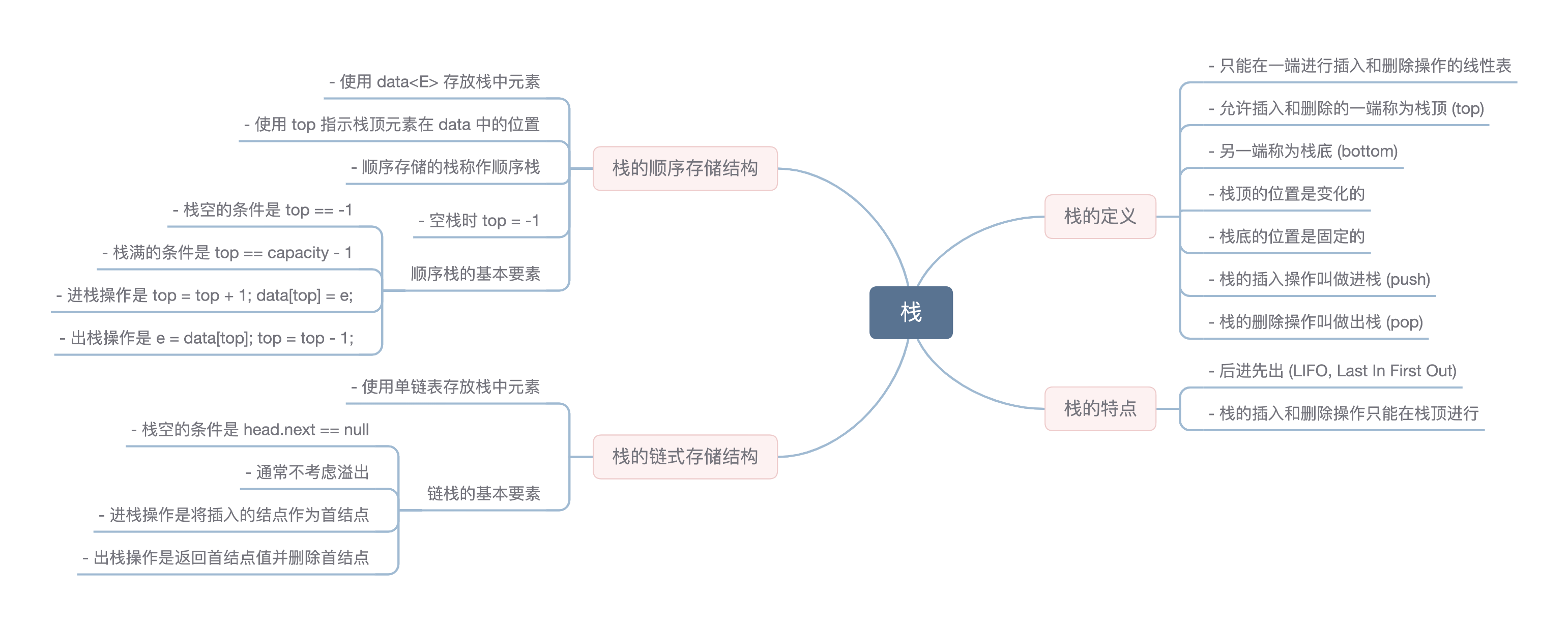
- 只能在一端进行插入和删除操作的线性表
- 允许插入和删除的一端称为栈顶 (top)
- 另一端称为栈底 (bottom)
- 栈顶的位置是变化的
- 栈底的位置是固定的
- 栈的插入操作叫做进栈 (push)
- 栈的删除操作叫做出栈 (pop)
### 栈的特点
- 后进先出 (LIFO, Last In First Out)
- 栈的插入和删除操作只能在栈顶进行
### 栈的抽象数据类型
ADT Stack {
数据对象
$ D = \lbrace a\_i | 0 \leq i \leq n-1, n \geq 0, 元素 a\_i 为 E 类型 \rbrace $
数据关系
$ r = \lbrace <a\_i, a\_{i+1}> | a\_i, a\_{i+1} \in D, i = 0, \dots, n-2 \rbrace $
基本运算
boolean empty();
void push(E e)
E pop();
E peek() }
### 栈的顺序存储结构
- 使用 `data<E>` 存放栈中元素
- 使用 `top` 指示栈顶元素在 data 中的位置
- 顺序存储的栈称作顺序栈
- 空栈时 `top = -1`
### 顺序栈的基本要素
- 栈空的条件是 `top == -1`
- 栈满的条件是 `top == capacity - 1`
- 进栈操作是 `top = top + 1; data[top] = e;`
- 出栈操作是 `e = data[top]; top = top - 1;`
### SqStackClass<E>
public class SqStackClass<E>
{
final int initcapacity=10;
private int capacity;
private E[] data;
private int top;
public SqStackClass()
{
data = (E[])new Object[initcapacity];
capacity=initcapacity;
top=-1;
}
}
### updatecapacity(int newcapacity)
private void updatecapacity(int newcapacity)
{
E[] newdata = (E[])new Object[newcapacity];
for (int i=0;i<top;i++)
newdata[i]=data[i];
capacity=newcapacity;
data=newdata;
}
### empty()
public boolean empty()
{
return top==-1;
}
### push(E e)
public void push(E e)
{
if (top==capacity-1)
updatecapacity(2*(top+1));
top++;
data[top]=e;
}
### pop()
public E pop()
{
if (empty())
throw new IllegalArgumentException("栈空");
E e=(E)data[top];
top--;
if (top+1>initcapacity && top+1==capacity/4)
updatecapacity(capacity/2);
return e;
}
### peek()
public E peek()
{
if (empty())
throw new IllegalArgumentException("栈空");
return (E)data[top];
}
### toString()
public String toString()
{
String ans="";
for (int i=0;i<=top;i++)
ans+=data[i].toString()+" ";
return ans;
}
### 栈的链式存储结构
- 使用单链表存放栈中元素
### 链栈的基本要素
- 栈空的条件是 `head.next == null`
- 通常不考虑溢出
- 进栈操作是将插入的结点作为首结点
- 出栈操作是返回首结点值并删除首结点
### LinkNode<E>
class LinkNode<E>
{
E data;
LinkNode<E> next;
public LinkNode()
{
next=null;
}
public LinkNode(E d)
{
data=d;
next=null;
}
}
### LinkStackClass<E>
public class LinkStackClass<E>
{
LinkNode<E> head;
public LinkStackClass()
{
head=new LinkNode<E>();
head.next=null;
}
}
### empty()
public boolean empty()
{
return head.next==null;
}
### push(E e)
public void push(E e)
{
LinkNode<E> s=new LinkNode<E>(e);
s.next=head.next;
head.next=s;
}
### pop()
public E pop()
{
if (empty())
throw new IllegalArgumentException("栈空");
E e=(E)head.next.data;
head.next=head.next.next;
return e;
}
### peek()
public E peek()
{
if (empty())
throw new IllegalArgumentException("栈空");
E e=(E)head.next.data;
return e;
}
### toString()
public String toString()
{
String ans="";
if (!empty())
{
LinkNode<E> p=head.next;
while (p!=null)
{
ans+=p.data+" ";
p=p.next;
}
}
return ans;
}
### 9.5 栈
- 栈在数据结构中是如何定义的?
- 描述栈的后进先出 (LIFO) 特性.
- 进栈和出栈具体是指什么?
- 顺序栈和链栈有什么区别?
- 空栈时, 栈顶指针 top 应该指向什么位置?
- 在链栈中, 栈空的条件是什么?
----
[ 9.3 线性表的链式存储结构](dbds-9-3.html#/overview)
[| 练习 |](dbds-exec.html)
[ 9.6 队列](dbds-9-6.html#/overview)