### 递归 Recursion - 一个过程或函数在其定义或说明中直接或间接调用自身的一种方法 - 通常把一个大型复杂问题层层转化为一个与原问题相似的规模较小的问题来求解

### 递归的数学原理 - 数学归纳法 - 证明当 $ n = 1 $ 时命题成立 - 假设当 $ n = k - 1 $ 时命题成立 - 证明当 $ n = k $ 时命题成立

### 例 - $$ 1 + 2 + 3 + \dots + n = \frac{n(n+1)}{2} $$ - 证明: - 1. 当 $ n = 1 $ 时，左边 $ = 1 $，右边 $ = \frac{1(1+1)}{2} = 1 $ - 2. 假设当 $ n = k - 1 $ 时命题成立，即 $ 1 + 2 + 3 + \dots + (k - 1) = \frac { k ( k - 1 ) }{ 2 } $ 成立 - 3. 当 $ n = k $ 时，左边 $ = 1 + 2 + 3 + \dots + k = \frac { k ( k - 1 ) }{ 2 } + k = \frac { k ( k - 1 ) }{ 2 } $，右边 $ = \frac { k ( k + 1 ) }{ 2 } $

### 递归的实现 int Fact(int n) { if (n == 0) return 1; else return n * Fact(n - 1); } - $ n! $ 的递归实现

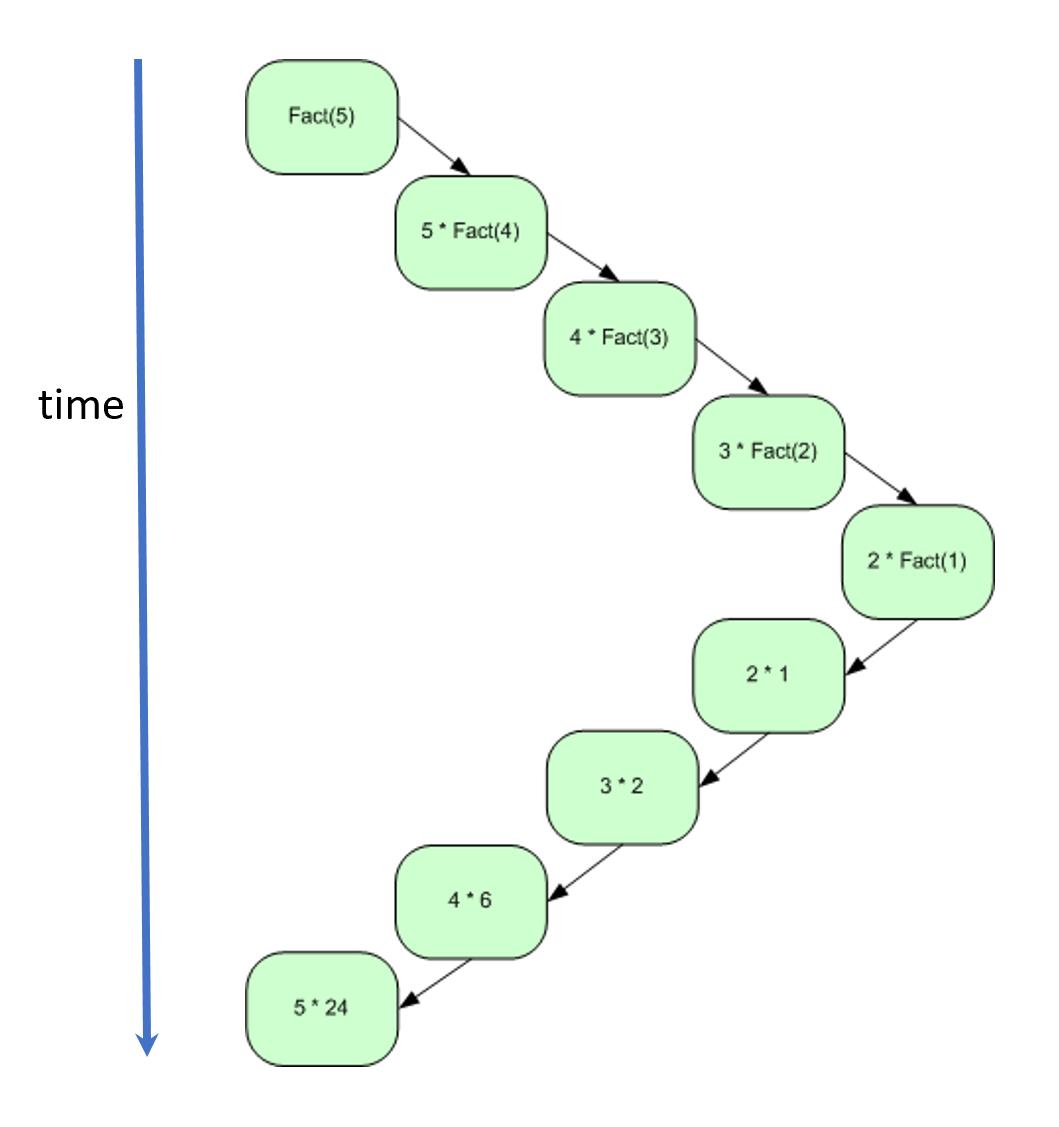
 #### n Factorial

### 递归的条件 - 问题可以转化为规模较小的同类问题 - 递归调用的次数要有穷 - 每次递归调用后问题规模应减少 - 必须有结束递归的条件

### 递归的复杂度 - 空间复杂度 $ = $ 递归深度 $ \times $ 每次递归所需的辅助空间 - 时间复杂度 $ = $ 每次递归所需时间 $ \times $ 递归调用次数

### 递归的应用 - 定义是递归的 - 数据结构是递归的 - 求解方法是递归的

### 定义是递归的 int fib(int n) { if (n == 1 || n == 2) return 1; else return fib(n - 1) + fib(n - 2); } - 斐波那契数列

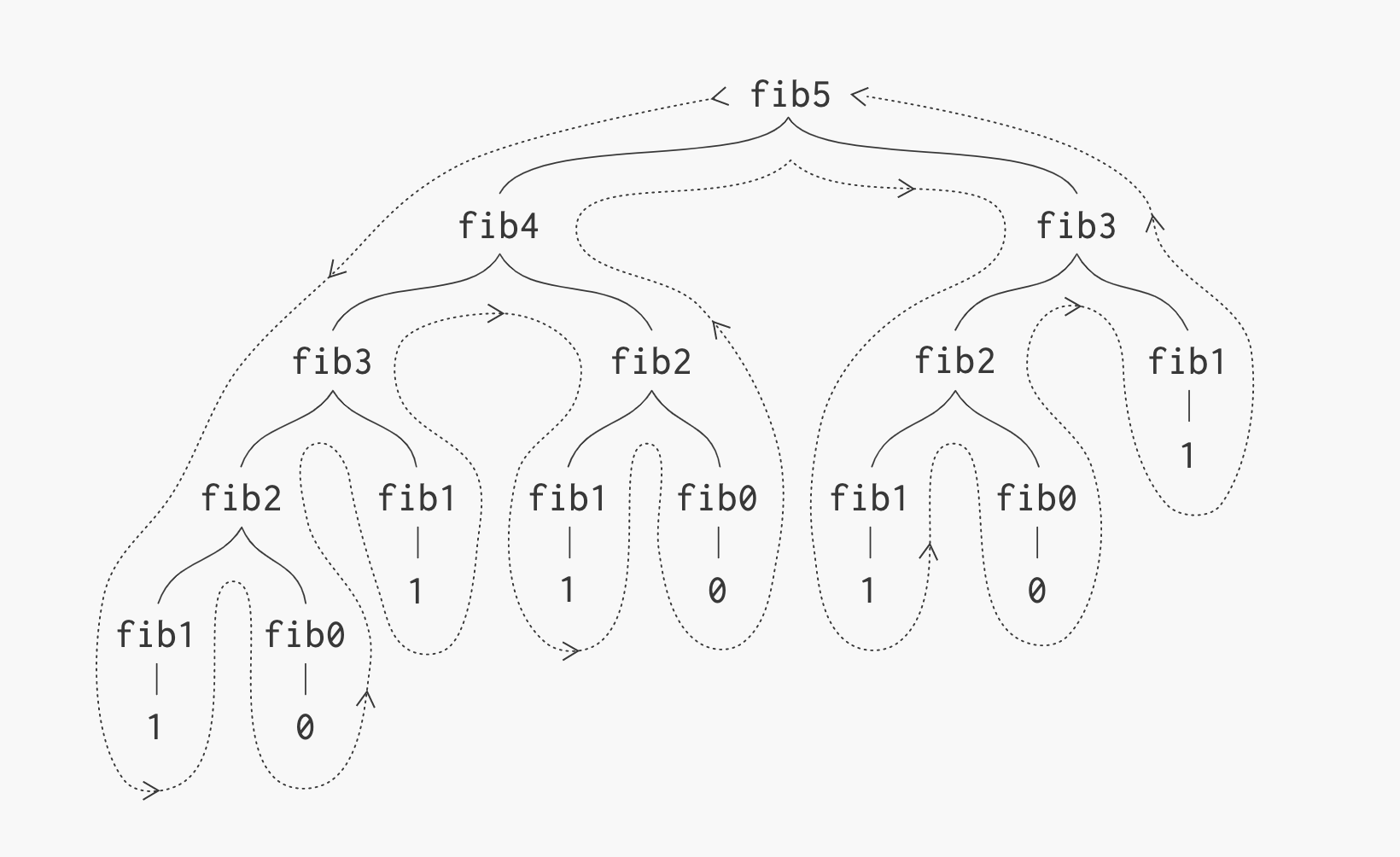
 #### Fibnoacci Sequence

### 数据结构是递归的 public static int Sum(LinkNode <integer> p) { if(p == null) return 0; else return p.data + Sum(p.next); } - 无头结点的单链表数据成员之和

### 求解方法是递归的 - 汉诺塔问题 Hanoi Tower - 每次只能移动一个盘片 - 盘片可以放在任何一根柱上 - 任何时候大盘在下小盘在上

 #### Hanoi Tower

### 汉诺塔问题的递归实现 void Hanoi(int n, char x, char y, char z) { if (n == 1) System.out.printf ("Move disk %d from %c to %c\n", n, x, z); else { Hanoi(n - 1, x, z, y); System.out.printf ("Move disk %d from %c to %c\n", n, x, z); Hanoi(n - 1, y, x, z); } }

### 递归模型 - $ n! $ 的递归模型 $$ \begin{align} f(n) & = 1, & n & = 0 \\\ f(n) & = n * f(n - 1), & n & > 0 \end{align} $$

 #### n Factorial

### 递归模型 - 斐波那契数列的递归模型 $$ \begin{align} f(n) & = 1, & n & = 1, 2 \\\ f(n) & = f(n - 1) + f(n - 2), & n & > 2 \end{align} $$

 #### Fibnoacci Sequence

### 递归模型的构成 - 递归出口 - 递归体

### 递归出口 - 递归的终止条件 - $ f(s\_1) = m\_1 $

### 递归体 - 递归的计算过程 - $ f(n) $ 与 $ f(n - 1) $ 的关系

### 递归的优缺点 - 逻辑简单 - 效率不高 - 空间复杂度高


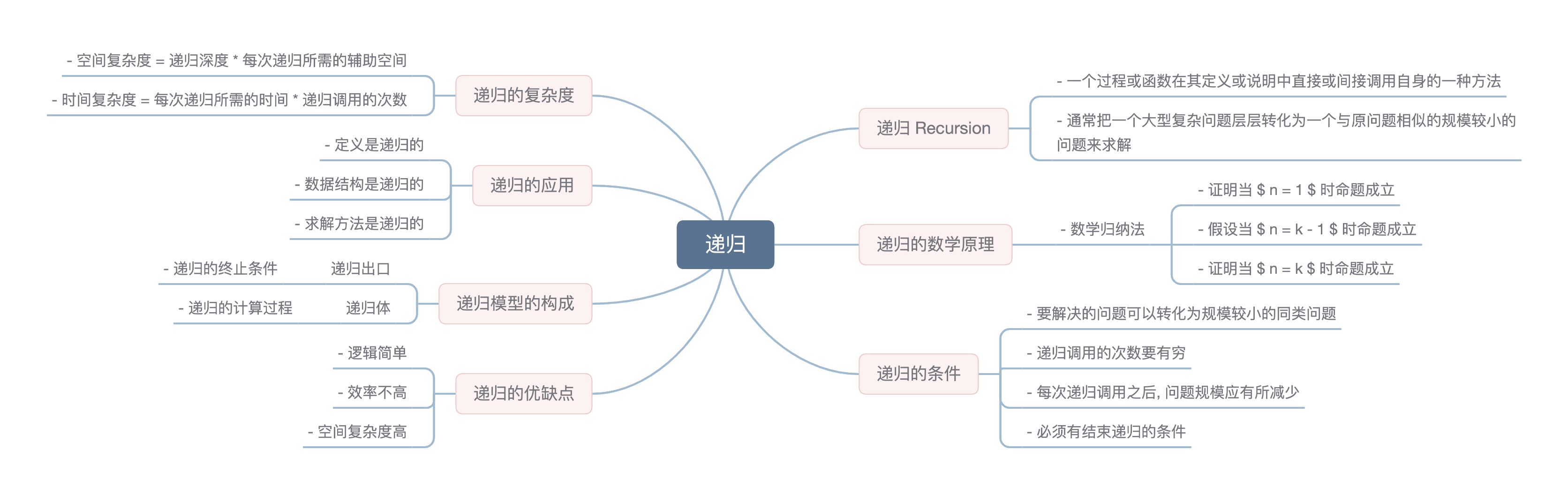
### 9.7 递归 - 递归是如何实现自我调用的? - 当递归深度非常大时可能会遇到哪些问题? - 数学归纳法与递归在逻辑上有何相似性? - 描述一种递归的数据结构. - 在递归算法中如何确保递归会终止? ---- [ 9.6 队列](dbds-9-6.html#/overview) [| 练习 |](dbds-exec.html) [ 10.1 树的基本概念](dbds-10-1.html#/overview)